题目内容
19．如图，在小正方形边长为1的网格中画出了某多面体的三视图，则该多面体的外接球表面积为48π．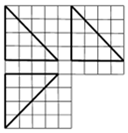
分析 根据三视图知几何体是三棱锥为正方体一部分，并求出棱长、画出直观图，由正方体的性质求出外接球的半径，代入球的表面积公式求值即可．
解答 解：根据三视图知几何体是：
三棱锥P-ABC为棱长为4的长方体一部分，
直观图如图所示：
则三棱锥P-ABC的外接球是此正方体的外接球，
设外接球的半径是R，
由正方体的性质可得，2R=$\sqrt{{4}^{2}+{4}^{2}+{4}^{2}}$=$4\sqrt{3}$，
则R=$2\sqrt{3}$
即该几何体外接球的表面积S=4πR2=48π，
故答案为：48π．
点评 本题考查由三视图求几何体外接球的表面积，在三视图与直观图转化过程中，以一个正方体为载体是很好的方式，使得作图更直观，考查空间想象能力．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
9．已知约束条件$\left\{\begin{array}{l}{x-3y+4≥0}\\{x+2y-1≥0}\\{3x+y-8≤0}\end{array}\right.$，若目标函数z=x+ay（a≥0）在且只在点（2，2）处取得最大值，则a的取值范围为（ ）
| A． | 0＜a＜$\frac{1}{3}$ | B． | a≥$\frac{1}{3}$ | C． | a＞$\frac{1}{3}$ | D． | 0＜a＜$\frac{1}{2}$ |
10．质地均匀的正四面体表面分别印有0，1，2，3四个数字，某同学随机的抛掷次正四面体2次，若正四面体与地面重合的表面数字分别记为m，n，且两次结果相互独立，互不影响．记m2+n2≤4为事件A，则事件A发生的概率为（ ）
| A． | $\frac{3}{8}$ | B． | $\frac{3}{16}$ | C． | $\frac{π}{8}$ | D． | $\frac{π}{16}$ |
4．
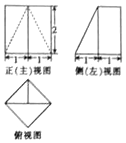已知一个几何体的三视图如图所示，则该几何体的体积为（ ）
已知一个几何体的三视图如图所示，则该几何体的体积为（ ）| A． | $\frac{32}{3}$ | B． | $\frac{16}{3}$ | C． | $\frac{8}{3}$ | D． | $\frac{4}{3}$ |
公元263年左右，我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率π，他从圆内接正六边形算起，令边数一倍一倍地增加，即12，24，48，…，192，…，逐个算出正六边形，正十二边形，正二十四边形，…，正一百九十二边形，…的面积，这些数值逐步地逼近圆面积，刘徽算到了正一百九十二边形，这时候π的近似值是3.141024，刘徽称这个方法为“割圆术”，并且把“割圆术”的特点概括为“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”．刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的，用有限来逼近无穷，这种思想及其重要，对后世产生了巨大影响，如图是利用刘徽的“割圆术”思想设计的一个程序框图，若运行改程序（参考数据：$\sqrt{3}$≈1.732，sin15°≈0.2588，sin7.5°≈0.1305），则输出n的值为（ ）