题目内容
已知函数f(x)是定义在R上的可导函数,其导函数记为f′(x),若对于任意实数x,有f(x)>f′(x),且y=f(x)-1为奇函数,则不等式f(x)<ex的解集为( )
| A、(-∞,0) |
| B、(0,+∞) |
| C、(-∞,e4) |
| D、(e4,+∞) |
考点:导数的运算
专题:导数的综合应用
分析:根据条件构造函数令g(x)=
,判断函数g(x)的单调性即可求出不等式的解集.
| f(x) |
| ex |
解答:
解:令g(x)=
,
则g′(x)=
=
,
∵f(x)>f′(x),
∴g′(x)<0,
即g(x)为减函数,
∵y=f(x)-1为奇函数,
∴f(0)-1=0,
即f(0)=1,g(0)=1,
则不等式f(x)<ex等价为
<1=g(0),
即g(x)<g(0),
解得x>0,
∴不等式的解集为(0,+∞),
故选:B.
| f(x) |
| ex |
则g′(x)=
| f′(x)ex-f(x)ex |
| [ex]2 |
| f′(x)-f(x) |
| ex |
∵f(x)>f′(x),
∴g′(x)<0,
即g(x)为减函数,
∵y=f(x)-1为奇函数,
∴f(0)-1=0,
即f(0)=1,g(0)=1,
则不等式f(x)<ex等价为
| f(x) |
| ex |
即g(x)<g(0),
解得x>0,
∴不等式的解集为(0,+∞),
故选:B.
点评:本题主要考查不等式的解法,利用条件构造函数,利用函数的单调性解不等式是解决本题的关键,考查学生的解题构造能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设1<x<2,则
、(
)2、
的大小关系是( )
| lnx |
| x |
| lnx |
| x |
| lnx2 |
| x2 |
A、(
| ||||||
B、
| ||||||
C、(
| ||||||
D、
|
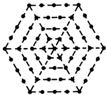 如图,有一个形如六边形的点阵,它的中心是一个点(算第1层),第2层每边有两个点,第3层每边有三个点,依此类推.
如图,有一个形如六边形的点阵,它的中心是一个点(算第1层),第2层每边有两个点,第3层每边有三个点,依此类推.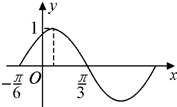 函数f(x)=sin(ωx+φ),(x∈R)(ω>0,|φ|<
函数f(x)=sin(ωx+φ),(x∈R)(ω>0,|φ|<