题目内容
已知直线y=kx+2和椭圆
+
=1，当k取何值时，直线与椭圆相交？相切？相离？
| x2 |
| 3 |
| y2 |
| 2 |
考点：椭圆的应用
专题：计算题,圆锥曲线的定义、性质与方程
分析：直线y=kx+2，代入椭圆
+
=1，整理可得（2+3k2）x2+12kx+6=0，根据△，可得结论．
| x2 |
| 3 |
| y2 |
| 2 |
解答：
解：直线y=kx+2，代入椭圆
+
=1，整理可得（2+3k2）x2+12kx+6=0，
∴△=（12k）2-24（2+3k2）=72k2-48
令72k2-48＞0，可得k＜-
或k＞
，直线与椭圆相交；
令72k2-48=0，可得k=±
，直线与椭圆相切；
令72k2-48＜0，可得-
＜k＜
，直线与椭圆相离．
| x2 |
| 3 |
| y2 |
| 2 |
∴△=（12k）2-24（2+3k2）=72k2-48
令72k2-48＞0，可得k＜-
| ||
| 3 |
| ||
| 3 |
令72k2-48=0，可得k=±
| ||
| 3 |
令72k2-48＜0，可得-
| ||
| 3 |
| ||
| 3 |
点评：本题考查椭圆的应用，考查直线与椭圆的位置关系，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
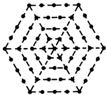如图，有一个形如六边形的点阵，它的中心是一个点（算第1层），第2层每边有两个点，第3层每边有三个点，依此类推．
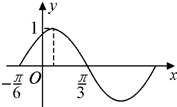函数f（x）=sin（ωx+φ），（x∈R）（ω＞0，|φ|＜