题目内容
11.已知a,b为实数,则“a=0”是“f(x)=x2+a|x|+b为偶函数”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 根据函数奇偶性的定义以及充分必要条件判断即可.
解答 解:a=0时,f(x)=x2+b为偶函数,是充分条件,
由f(-x)=(-x)2+a|-x|+b=f(x),得f(x)是偶函数,
故a=0”是“f(x)=x2+a|x|+b为偶函数”的充分不必要条件,
故选:A.
点评 本题考查了充分必要条件,考查函数的奇偶性,是一道基础题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
1.函数f(x)=sin(ωx+φ),(|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )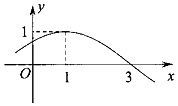

| A. | (-1+4kπ,1+4kπ),k∈Z | B. | (-3+8kπ,1+8kπ),k∈Z | ||
| C. | (-1+4k,1+4k),k∈Z | D. | (-3+8k,1+8k),k∈Z |
6.已知函数f(x)在R上满足f(x)=2f(2-x)-x2+8x-8,则曲线y=f(x)在点(1,f(1))处的切线方程是( )
| A. | y=-2x+3 | B. | y=x | C. | y=3x-2 | D. | y=2x-1 |
2.已知函数f(x)=$\frac{2}{3}$x3-2ax2-3x(a∈R),若函数f(x)的图象上点P(1,m)处的切线方程为3x-y+b=0,则m的值为( )
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
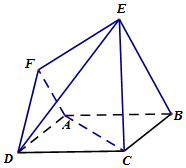 在如图所示的六面体中,面ABCD是边长为2的正方形,面ABEF是直角梯形,∠FAB=90°,AF∥BE,BE=2AF=4.
在如图所示的六面体中,面ABCD是边长为2的正方形,面ABEF是直角梯形,∠FAB=90°,AF∥BE,BE=2AF=4.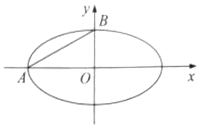 已知点A(-2,0),B(0,1)在椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上.
已知点A(-2,0),B(0,1)在椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上.