题目内容
19.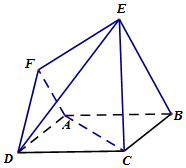 在如图所示的六面体中,面ABCD是边长为2的正方形,面ABEF是直角梯形,∠FAB=90°,AF∥BE,BE=2AF=4.
在如图所示的六面体中,面ABCD是边长为2的正方形,面ABEF是直角梯形,∠FAB=90°,AF∥BE,BE=2AF=4.(Ⅰ)求证:AC∥平面DEF;
(Ⅱ)若二面角E-AB-D为60°,求直线CE和平面DEF所成角的正弦值.
分析 (1)、连接AC,BD相交于点O,取DE的中点为G,连接FG,OG.只证AC∥FG,即可‘
(2)先证EC⊥平面ABCD,再以C为坐标原点,CB为x轴、CD为y轴、CE为z轴建立空间直角坐标系即可
解答 证明:(1)连接AC,BD相交于点O,取DE的中点为G,连接FG,OG.
∵ABCD是正方形,∴O是DB的中点,∴OG∥BE,OG=$\frac{1}{2}BE$,
又因为AF∥BE,AF=$\frac{1}{2}BE$,所以OG∥AF且OG=AF,
所以四边形AOGF是平行四边形,(3分)
∴AC∥FG,又因为FG?平面DEF,AC?平面EDF
∴AC∥平面DEF(5分)
(2)∵ABCD是正方形,ABEF是直角梯形,∠FAB=90°,∴DA⊥AB,FA⊥AB
∵AD∩AF=A,∴AB⊥平面AFD,同理可得AB⊥平面EBC.
又∵AB?平面ABCD,所以平面AFD⊥平面ABCD,
又因为二面角E-AB-D为600,
所以∠FAD=∠EBC=60°,BE=2AF=4,BC=2,由余弦定理得EC=2$\sqrt{3}$,
所以EC⊥BC,又因为AB⊥平面EBC,∴EC⊥AB,所以EC⊥平面ABCD,(7分)
法一:以C为坐标原点,CB为x轴、CD为y轴、CE为z轴建立空间直角坐标系.则C(0,0,0),D(0,2,0),E(0,0,2$\sqrt{3}$),F(1,2,$\sqrt{3}$),(8分)
所以$\overrightarrow{CE}=(0,0,2\sqrt{3})$,$\overrightarrow{DF}=(1,0,\sqrt{3})$,$\overrightarrow{EF}(1,2,-\sqrt{3})$,设平面DEF的一个法向量为$\overrightarrow{n}=(x,y,z)$,则$\overrightarrow{n}•\overrightarrow{DF}=0,\overrightarrow{n}•\overrightarrow{EF}=0$即$\left\{\begin{array}{l}{x+\sqrt{3}z=0}\\{x+2y-\sqrt{3}z=0}\end{array}\right.$令z=$\sqrt{3}$,则x=-3,y=3,
所以$\overrightarrow{n}=(-3,3,\sqrt{3})$(11分)
设直线CE和平面DEF所成角为θ,
则sinθ=|cos$<\overrightarrow{CE},\overrightarrow{n}>$=$\frac{\sqrt{7}}{7}$|(12分)
点评 本题考查立体几何中的线面关系,空间角,空间向量在立体几何中的应用等基础知识,考查运算求解能力、空间想象能力、等价转化能力,考查数形结合思想、化归与转化、或然与必然等数学思想,属于中档题.

| A. | $\frac{{\sqrt{3}}}{2}π$ | B. | $\frac{3}{2}π$ | C. | 3π | D. | 12π |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
| A. | 10 | B. | 15 | C. | 20 | D. | 21 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |