题目内容
a>b是|a|>b的 条件.
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:充分性分成b<0和b≥0讨论;必要性举反例即可否定.
解答:
解:充分性:当b<0时,|a|≥0>b;当b≥0时,a>b≥0⇒|a|>b,则a>b⇒|a|>b,充分性满足;
必要性:令a=-2,b=-1满足|a|>b,但不满足a>b,必要性不成立;
综上,a>b是|a|>b的充分不必要条件,
故答案为:充分不必要.
必要性:令a=-2,b=-1满足|a|>b,但不满足a>b,必要性不成立;
综上,a>b是|a|>b的充分不必要条件,
故答案为:充分不必要.
点评:本题考查充要条件,首先要判断条件和结论,然后分成充分性和必要性讨论,注意可举反例否定结论.

练习册系列答案
相关题目
若函数f(x)=
,则f(f(e))=( )(其中e为自然对数的底数)
|
| A、1 | B、2 | C、e | D、5 |
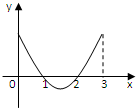 函数f(x)定义域为[0,3],导函数f′(x)在[0,3]内图象如图所示,则函数f(x)在[0,3]的单调递减区间为( )
函数f(x)定义域为[0,3],导函数f′(x)在[0,3]内图象如图所示,则函数f(x)在[0,3]的单调递减区间为( )| A、[0,1] |
| B、[1,2] |
| C、[2,3] |
| D、[0,2] |
