题目内容
7.已知角α的终边上一点的坐标为(sin$\frac{π}{6}$,cos$\frac{π}{6}$),则角α的最小正值为$\frac{π}{3}$.分析 由条件利用任意角的三角函数的定义求得tanα的值,可得角α的最小正值.
解答 解:角α的终边上一点的坐标为(sin$\frac{π}{6}$,cos$\frac{π}{6}$),即($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
则由任意角的三角函数的定义,可得tanα=$\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}$=$\sqrt{3}$,
则角α的最小正值为$\frac{π}{3}$,
故答案为:$\frac{π}{3}$.
点评 本题主要考查任意角的三角函数的定义,根据三角函数的值求角,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.在△ABC中,B=45°,C=60°,c=1,则b=( )
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
18.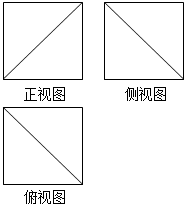 已知某几何体的三视图都是边长为6的正方形,如图所示,则该几何体的体积是( )
已知某几何体的三视图都是边长为6的正方形,如图所示,则该几何体的体积是( )
 已知某几何体的三视图都是边长为6的正方形,如图所示,则该几何体的体积是( )
已知某几何体的三视图都是边长为6的正方形,如图所示,则该几何体的体积是( )| A. | 180 | B. | 144 | C. | 92 | D. | 180或144 |
15.一个算法程序框图如图所示,其输出结果为( )


| A. | 9 | B. | 25 | C. | 36 | D. | 49 |
19.已知⊙O1与⊙O2的半径分别为R、r,且它们是方程x2-9x+14=0的两根,若⊙O1与⊙O2相切,则圆心距O1O2等于( )
| A. | 5 | B. | 9 | C. | 5或9 | D. | 10或18 |
17.在复平面内,复数z和$\frac{1+i}{1-2i}$所表示的点关于虚轴对称,则z=( )
| A. | -$\frac{1}{5}$+$\frac{3}{5}$i | B. | $\frac{1}{5}$+$\frac{3}{5}$i | C. | $\frac{1}{5}$-$\frac{3}{5}$i | D. | -$\frac{1}{5}$-$\frac{3}{5}$i |
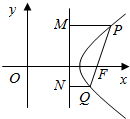 如图,点F是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,过点F的直线的斜率为3,与双曲线交于P,Q两点,分别过P、Q向右准线作垂线,垂足分别为M,N,且$\overrightarrow{PM}$=3$\overrightarrow{QN}$,求双曲线的离心率的大小.
如图,点F是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,过点F的直线的斜率为3,与双曲线交于P,Q两点,分别过P、Q向右准线作垂线,垂足分别为M,N,且$\overrightarrow{PM}$=3$\overrightarrow{QN}$,求双曲线的离心率的大小.