题目内容
3．已知方程x+$\frac{{e}^{2}}{x}$+m=0有大于0的实数解，求实数m的取值范围．分析 方程x+$\frac{{e}^{2}}{x}$+m=0可化为-m=x+$\frac{{e}^{2}}{x}$，利用基本不等式，即可求实数m的取值范围．
解答 解：方程x+$\frac{{e}^{2}}{x}$+m=0可化为-m=x+$\frac{{e}^{2}}{x}$，
∵x＞0，
∴x+$\frac{{e}^{2}}{x}$≥2e，当且仅当x=$\frac{{e}^{2}}{x}$，即x=e时取等号，
∴-m≥2e，
∴m≤-2e．
点评 本题考查求实数m的取值范围，考查基本不等式的运用，属于中档题．
练习册系列答案
相关题目
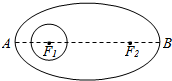1998年12月19日，太原卫星发射中心为摩托罗拉公司（美国）发射了“铱星”系统通信卫星，卫星运行的轨道是椭圆，F1、F2是其焦点，地球中心为焦点F1，设地球半径为m，已知椭圆轨道的近地点A（离地面最近的点）距地面$\frac{m}{3}$，远地点B（离地面最远的点）距地面3m，并且F1、A、B在同一直线上，求卫星运行的轨道方程．