题目内容
1.下列结论中正确的是②③④.(写出所有正确结论的序号)①若$\overrightarrow a•\overrightarrow b=0$,则$\overrightarrow a=0$或$\overrightarrow b=0$;
②若$|\overrightarrow a•\overrightarrow b|=|\overrightarrow a|•|\overrightarrow b|$,则$\overrightarrow a∥\overrightarrow b$;
③若$\overrightarrow a•\overrightarrow b=0$,则$|\overrightarrow a+\overrightarrow b|=|\overrightarrow a-\overrightarrow b|$;
④在△ABC中,点M满足$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow 0$,若存在实数λ使得$\overrightarrow{AB}+\overrightarrow{AC}=λ•\overrightarrow{AM}$成立,则λ=3.
分析 由$\overrightarrow a•\overrightarrow b=0$得出$\overrightarrow a=0$或$\overrightarrow b=0$或$\overrightarrow{a}$⊥$\overrightarrow{b}$,判断①错误;
由$|\overrightarrow a•\overrightarrow b|=|\overrightarrow a|•|\overrightarrow b|$得出|cosθ|=1,判断②正确;
由$\overrightarrow a•\overrightarrow b=0$得出$|\overrightarrow a+\overrightarrow b|=|\overrightarrow a-\overrightarrow b|$,判断③正确;
由$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow 0$得出M为△ABC的重心,得出$\overrightarrow{AM}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),判断④正确.
解答 解:对于①,当$\overrightarrow a•\overrightarrow b=0$时,$\overrightarrow a=0$或$\overrightarrow b=0$或$\overrightarrow{a}$⊥$\overrightarrow{b}$,∴①错误;
对于②,当$|\overrightarrow a•\overrightarrow b|=|\overrightarrow a|•|\overrightarrow b|$时,|cosθ|=1,∴$\overrightarrow a∥\overrightarrow b$,②正确;
对于③,当$\overrightarrow a•\overrightarrow b=0$时,$\overrightarrow a=0$或$\overrightarrow b=0$或$\overrightarrow{a}$⊥$\overrightarrow{b}$,∴$|\overrightarrow a+\overrightarrow b|=|\overrightarrow a-\overrightarrow b|$,③正确;
对于④,△ABC中,点M满足$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow 0$,
根据三角形重心的性质得,M为△ABC的重心;
∴$\overrightarrow{AM}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
∴$\overrightarrow{AB}$+$\overrightarrow{AC}$=3$\overrightarrow{AM}$,λ=3,④正确.
综上,正确的命题是②③④.
故答案为:②③④.
点评 本题考查了平面向量的数量积与应用问题,也考查了三角形重心的应用问题,是基础题目.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 已知线段AB上有9个确定的点(包括端点A与B).现对这些点进行往返标数(从A→B→A→B→…进行标数,遇到同方向点不够数时就“调头”往回数).如图:在点A上标1称为点1,然后从点1开始数到第二个数,标上2,称为点2,再从点2开始数到第三个数,标上3,称为点3(标上数n的点称为点n),…,这样一直继续下去,直到1,2,3,…,2013都被标记到点上.则点2013上的所有标记的数中,最小的是2.
已知线段AB上有9个确定的点(包括端点A与B).现对这些点进行往返标数(从A→B→A→B→…进行标数,遇到同方向点不够数时就“调头”往回数).如图:在点A上标1称为点1,然后从点1开始数到第二个数,标上2,称为点2,再从点2开始数到第三个数,标上3,称为点3(标上数n的点称为点n),…,这样一直继续下去,直到1,2,3,…,2013都被标记到点上.则点2013上的所有标记的数中,最小的是2. 某工厂生产A,B两种型号的产品,每种型号的产品在出厂时按质量分为一等品和二等品,为便于掌握生产状况,质检时将产品分为每20件一组,分别记录每组一等品的件数.现随机抽取了5组的质检记录,其一等品数茎叶图如图所示:
某工厂生产A,B两种型号的产品,每种型号的产品在出厂时按质量分为一等品和二等品,为便于掌握生产状况,质检时将产品分为每20件一组,分别记录每组一等品的件数.现随机抽取了5组的质检记录,其一等品数茎叶图如图所示:
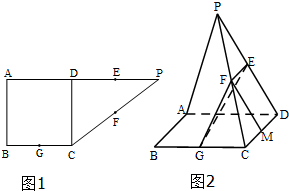 如图,在直角梯形ABCP中,AB=BC=3,AP=7,CD⊥AP于D,现将△PCD沿线段CD折成60°的二面角P-CD-A,设E,F,G分别是PD,PC,BC的中点.
如图,在直角梯形ABCP中,AB=BC=3,AP=7,CD⊥AP于D,现将△PCD沿线段CD折成60°的二面角P-CD-A,设E,F,G分别是PD,PC,BC的中点.
 如图,在圆C:(x+1)2+y2=16内有一点A(1,0),Q为圆C上一点,AQ的垂直平分线与C、Q的连线交于点M.
如图,在圆C:(x+1)2+y2=16内有一点A(1,0),Q为圆C上一点,AQ的垂直平分线与C、Q的连线交于点M.