题目内容
11. 如图,在圆C:(x+1)2+y2=16内有一点A(1,0),Q为圆C上一点,AQ的垂直平分线与C、Q的连线交于点M.
如图,在圆C:(x+1)2+y2=16内有一点A(1,0),Q为圆C上一点,AQ的垂直平分线与C、Q的连线交于点M.(1)求点M的轨迹方程;
(2)在x轴上是否存在一定点N(t,0),使得点M与点N的距离和它到直线l:x=4的距离的比是常数λ?若存在,求出点N及λ.
分析 (1)确定点M的轨迹是以(1,0),(-1,0)为焦点的椭圆,即可求点M的轨迹方程;
(2)由题意,$\frac{|MN|}{d}$=$\frac{\sqrt{(x-t)^{2}+{y}^{2}}}{|x-4|}$=$\sqrt{\frac{\frac{1}{4}{x}^{2}-2tx+({t}^{2}+3)}{{x}^{2}-8x+16}}$,由此可得比值,即可得出结论.
解答 解:(1)由题意知,点M在线段CQ上,从而有|CQ|=|MQ|+|MC|.
又点M在AQ的垂直平分线上,则|MA|=|MQ|,
∴|MA|+|MC|=|CQ|=4.∵A(1,0),C(-1,0),
∴点M的轨迹是以(1,0),(-1,0)为焦点的椭圆,
所以2a=4,a=2,b=$\sqrt{3}$
∴椭圆方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1…(6分)
(2)由题意,$\frac{|MN|}{d}$=$\frac{\sqrt{(x-t)^{2}+{y}^{2}}}{|x-4|}$=$\sqrt{\frac{\frac{1}{4}{x}^{2}-2tx+({t}^{2}+3)}{{x}^{2}-8x+16}}$,
∴$\frac{\frac{1}{4}}{1}=\frac{2t}{8}=\frac{{t}^{2}+3}{16}$,∴$t=1,λ=\frac{1}{2}$,即N(1,0),$λ=\frac{1}{2}$…(12分)
点评 本题考查椭圆的定义与方程,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
2.已知A∈α,AB=5,$AC=2\sqrt{2}$,且AB与α所成角的正弦值为$\frac{4}{5}$,AC与α所成的角为45°,点B,C在平面α同侧,则BC长的范围为( )
| A. | $[5-2\sqrt{2},5+2\sqrt{2}]$ | B. | $[\sqrt{5},\sqrt{29}]$ | C. | $[\sqrt{5},\sqrt{61}]$ | D. | $[\sqrt{29},\sqrt{61}]$ |
3.已知函数f(x)=x2-2ax+5(a>1),g(x)=log3x,若函数f(x)的定义域与值域都是[1,a],则对于任意的x1,x2∈[1,a+1]时,总有$|{f({x_1})-g({x_2})}|≤{t^2}+2t-1$恒成立,则t的取值范围为( )
| A. | [1,3] | B. | [-1,3] | C. | [1,+∞)∪(-∞,-3] | D. | [3,+∞)∪(-∞,-1] |
20.已知圆C:x2+y2+2x-3=0,直线l:x+ay+2-a=0(a∈R),则( )
| A. | l与C相离 | B. | l与C相切 | ||
| C. | l与C相交 | D. | 以上三个选项均有可能 |
1.执行如图所示的程序框图,则输出s的值为( )
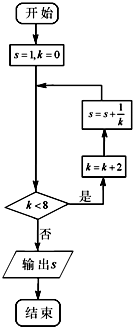

| A. | $\frac{3}{2}$ | B. | $\frac{7}{4}$ | C. | $\frac{23}{12}$ | D. | $\frac{49}{24}$ |
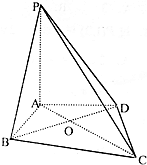 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BCD=60°,DC=BC=$\sqrt{3}$,AC和BD交于O点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BCD=60°,DC=BC=$\sqrt{3}$,AC和BD交于O点. 如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别 是PC,PD,BC的中点.
如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别 是PC,PD,BC的中点.