题目内容
10.已知R上的可导函数f(x)的图象如图所示,则不等式xf′(x)>0的解集为(-1,0)∪(1,+∞).
分析 根据导数与单调性的关系,可以确定x与f′(x)同正负的区间即可.
解答 解:由图可知函数f(x)在(-∞,-1),(1,+∞)单调递增,∴在(-∞,-1),(1,+∞)区间f′(x)>0,在(-1,1)函数f(x)单调递减,
∴f′(x)<0,所以x与f′(x)同正负的区间有:(-1,0 ),(1,+∞),
故不等式xf′(x)>0的解集为:(-1,0 )∪(1,+∞),
故答案为:(-1,0 )∪(1,+∞)
点评 本题考查了函数单调性与导数的关系,属于基础题.

练习册系列答案
相关题目
15. 如果执行如图所示的程序框图,则输出的结果为( )
如果执行如图所示的程序框图,则输出的结果为( )
 如果执行如图所示的程序框图,则输出的结果为( )
如果执行如图所示的程序框图,则输出的结果为( )| A. | 5 | B. | 7 | C. | 8 | D. | 13 |
2.已知A∈α,AB=5,$AC=2\sqrt{2}$,且AB与α所成角的正弦值为$\frac{4}{5}$,AC与α所成的角为45°,点B,C在平面α同侧,则BC长的范围为( )
| A. | $[5-2\sqrt{2},5+2\sqrt{2}]$ | B. | $[\sqrt{5},\sqrt{29}]$ | C. | $[\sqrt{5},\sqrt{61}]$ | D. | $[\sqrt{29},\sqrt{61}]$ |
20.已知圆C:x2+y2+2x-3=0,直线l:x+ay+2-a=0(a∈R),则( )
| A. | l与C相离 | B. | l与C相切 | ||
| C. | l与C相交 | D. | 以上三个选项均有可能 |
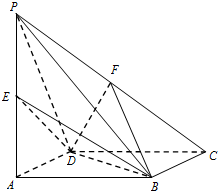 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E、F分别是PA、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E、F分别是PA、PC的中点.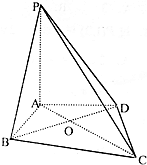 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BCD=60°,DC=BC=$\sqrt{3}$,AC和BD交于O点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BCD=60°,DC=BC=$\sqrt{3}$,AC和BD交于O点.