题目内容
9. 已知线段AB上有9个确定的点(包括端点A与B).现对这些点进行往返标数(从A→B→A→B→…进行标数,遇到同方向点不够数时就“调头”往回数).如图:在点A上标1称为点1,然后从点1开始数到第二个数,标上2,称为点2,再从点2开始数到第三个数,标上3,称为点3(标上数n的点称为点n),…,这样一直继续下去,直到1,2,3,…,2013都被标记到点上.则点2013上的所有标记的数中,最小的是2.
已知线段AB上有9个确定的点(包括端点A与B).现对这些点进行往返标数(从A→B→A→B→…进行标数,遇到同方向点不够数时就“调头”往回数).如图:在点A上标1称为点1,然后从点1开始数到第二个数,标上2,称为点2,再从点2开始数到第三个数,标上3,称为点3(标上数n的点称为点n),…,这样一直继续下去,直到1,2,3,…,2013都被标记到点上.则点2013上的所有标记的数中,最小的是2.
分析 确定标有2013的是1+2+3+…+2013=2027091号,2027091除以16的余数为3,即线段的第3个点标为2013,那么3+16n=1+2+3+…+k=$\frac{k(k+1)}{2}$,即3+32n=k(k+1),令n=0,即可得结论.
解答 解:记标有1为第1号,由于对这些点进行往返标数(从A→B→A→B→…进行标数,遇到同方向点不够数时就“调头”往回数),则标有2的是1+2号,标有3的是1+2+3号,标有4的是1+2+3+4,…,标有2013的是1+2+3+…+2013=2027091号.考虑为一圆周,则圆周上共16个点,
所以2027091除以16的余数为3,即线段的第3个点标为2013,那么3+16n=1+2+3+…+k=$\frac{k(k+1)}{2}$,
即3+32n=k(k+1).
当n=0时,k(k+1)=3,k=2满足题意,随着n的增大,k也增大.
所以,标有2013的那个点上标出的最小数为2.
故答案为:2.
点评 本题考查合情推理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知球的直径SC=4,A,B是该球球面上的两点,∠ASC=∠BSC=30°,且AB=$\sqrt{3}$,则三棱锥S-ABC的体积为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
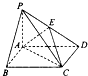 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.

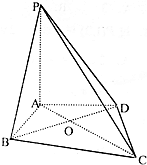 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BCD=60°,DC=BC=$\sqrt{3}$,AC和BD交于O点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BCD=60°,DC=BC=$\sqrt{3}$,AC和BD交于O点.