题目内容
已知函数f(x)=lnx-ax+
-1(a∈R).
(1)当a=-1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)当a≤12时,讨论f(x)的单调性.
| 1-a |
| x |
(1)当a=-1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)当a≤12时,讨论f(x)的单调性.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)把a=-1代入函数解析式,求出函数导函数,得到函数在x=2时的导数,再求出f(2),然后利用直线方程的点斜式得答案;
(2)确定函数的定义域,求出原函数的导函数,然后对a分类讨论,利用导数的正负,可确定函数的单调性.
(2)确定函数的定义域,求出原函数的导函数,然后对a分类讨论,利用导数的正负,可确定函数的单调性.
解答:
解:(1)由f(x)=lnx-ax+
-1,得
f′(x)=
,当a=-1时,f′(x)=
,
则f′(2)=
=1,
又f(2)=ln2+2+
-1=ln2+2,
∴曲线y=f(x)在点(2,f(2))处的切线方程为y-ln2-2=1×(x-2),
即x-y+ln2=0;
(2)函数f(x)的定义域为(0,+∞),
f′(x)=
,
当a=0时,f′(x)=
,
令f′(x)=
<0,∵x>0,∴0<x<1,
∴函数f(x)在(1,+∞)上是增函数,在(0,1)上是减函数;
当a<0时,令f′(x)=
>0,得-ax2+x-1+a>0,解得x>1或x<
-1(舍去),
此时函数f(x)在(1,+∞)上是增函数,在(0,1)上是减函数;
当0<a<
时,令f′(x)=
>0,得-ax2+x-1+a>0,解得1<x<
-1,
此时函数f(x)在(1,
-1)上是增函数,在(0,1)和(
-1,+∞)上是减函数;
当a=
时,f′(x)=
=-
(x-1)2≤0,
此时函数f(x)在(0,+∞)上是减函数.
综上,当a≤0时,函数f(x)在(1,+∞)上是增函数,在(0,1)上是减函数;
当0<a<
时,函数f(x)在(1,
-1)上是增函数,在(0,1)和(
-1,+∞)上是减函数;
当a=
时,函数f(x)在(0,+∞)上是减函数.
| 1-a |
| x |
f′(x)=
| -ax2+x+a-1 |
| x2 |
| x2+x-2 |
| x2 |
则f′(2)=
| 22+2-2 |
| 22 |
又f(2)=ln2+2+
| 2 |
| 2 |
∴曲线y=f(x)在点(2,f(2))处的切线方程为y-ln2-2=1×(x-2),
即x-y+ln2=0;
(2)函数f(x)的定义域为(0,+∞),
f′(x)=
| -ax2+x+a-1 |
| x2 |
当a=0时,f′(x)=
| x-1 |
| x2 |
令f′(x)=
| x-1 |
| x2 |
∴函数f(x)在(1,+∞)上是增函数,在(0,1)上是减函数;
当a<0时,令f′(x)=
| -ax2+x+a-1 |
| x2 |
| 1 |
| a |
此时函数f(x)在(1,+∞)上是增函数,在(0,1)上是减函数;
当0<a<
| 1 |
| 2 |
| -ax2+x+a-1 |
| x2 |
| 1 |
| a |
此时函数f(x)在(1,
| 1 |
| a |
| 1 |
| a |
当a=
| 1 |
| 2 |
-
| ||||
| x2 |
| 1 |
| 2x2 |
此时函数f(x)在(0,+∞)上是减函数.
综上,当a≤0时,函数f(x)在(1,+∞)上是增函数,在(0,1)上是减函数;
当0<a<
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a |
当a=
| 1 |
| 2 |
点评:本题考查利用导数求过曲线上某点处的切线方程,考查了利用导数研究函数的单调性,关键是做到对a正确分类,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
若直线ax+by=1与不等式
,表示的平面区域无公共点,则2a+3b的取值范围是( )
|
| A、(-7,1) | B、(-3,5) |
| C、(-7,3) | D、R |
已知数列{an}是公差不为0的等差数列,Sn是它的前n项和,a1,a3,a4成等比数列,若a2n=3Sn,则n=( )
| A、10 | B、12 | C、14 | D、16 |
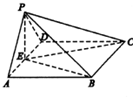 如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是等边三角形,平面PAD⊥平面ABCD,E是线段AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是等边三角形,平面PAD⊥平面ABCD,E是线段AD的中点.