题目内容
设f(x)=lnx,g(x)=f(x)+f ′(x).
(1)求g(x)的单调区间和最小值;
(2)讨论g(x)与g(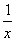 )的大小关系;
)的大小关系;
(3)求a的取值范围,使得g(a)-g(x)<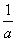 对任意x>0成立.
对任意x>0成立.
[解析] (1)g′(x)=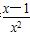 ,由g′(x)>0,得g(x)的单调增区间为(1,+∞);由g′(x)<0,得g(x)的单调减区间为(0,1).因此x=1是g(x)的唯一极值点,且为极小值点,从而是最小值点.所以g(x)min=g(1)=1.
,由g′(x)>0,得g(x)的单调增区间为(1,+∞);由g′(x)<0,得g(x)的单调减区间为(0,1).因此x=1是g(x)的唯一极值点,且为极小值点,从而是最小值点.所以g(x)min=g(1)=1.
(2)设h(x)=g(x)-g(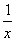 ),则h′(x)=-
),则h′(x)=-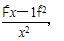 ,
,
h′(x)≤0,∴h(x)在(0,+∞)上为减函数.
当x=1时,h(1)=0,即g(x)=g(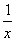 );
);
当0<x<1时,h(x)>h(1)=0,即g(x)>g(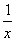 );
);
当x>1时,h(x)<h(1)=0,即g(x)<g(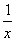 ).
).
(3)由(1)知g(x)的最小值为1,所以g(a)-g(x)<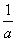 ,对任意x>0成立⇔由g(a)-1<
,对任意x>0成立⇔由g(a)-1<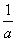 ,得0<a<e.
,得0<a<e.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
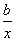 ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.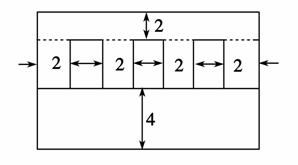
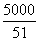 m B.长150m,宽66m
m B.长150m,宽66m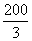 m
m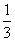 x3+
x3+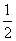 x2+2ax.
x2+2ax.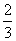 ,+∞)上存在单调递增区间,求a的取值范围.
,+∞)上存在单调递增区间,求a的取值范围.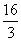 ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值.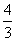 B.2
B.2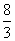 D.
D.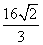
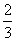 π的终边上,且|OP|=2,则点P的坐标为________.
π的终边上,且|OP|=2,则点P的坐标为________.