题目内容

15．参数方程$\left\{\begin{array}{l}{x=t-1}\\{y={t}^{2}+2}\end{array}\right.$（t∈R）表示的曲线是（　　）
A．经过坐标原点B．与x轴相交，但与y轴不相交
C．与y轴相交，但与x轴不相交D．不经过坐标原点，但与x轴、y轴相交

分析 将参数方程化成普通方程判断．

解答 解：由x=t-1得t=x+1，将t=x+1代入y=t2+2得y=x2+2x+3，
∴曲线表示开口向上的抛物线，∴抛物线与y轴相交．
∵△=22-12=-8＜0，∴抛物线与x轴不相交．
当x=0时，y=3≠0，故抛物线不经过原点，
故选：C．

点评 本题考查了参数方程与普通方程的互化，抛物线的性质，属于基础题．

练习册系列答案
相关题目
20．如图所示，在正方体ABCD-A1B1C1D1中，
（1）判断直线A1B1与DC是否平行？
（2）判断直线A1A与平面ABCD是否垂直？
（3）判断直线BC1与平面ADD1A1是否平行？
1．已知递增等差数列{an}满足a1+a5=4，前3项的积为8，求等差数列{an}的通项公式．
3．已知函数g（x）=$\frac{2}{x}$+lnx，f（x）=mx-$\frac{m-2}{x}$-lnx，m∈R．
（1）求函数g（x）的单调区间和极值；
（2）若f（x）-g（x）在[1，+∞）上为单调函数，求m的取值范围．
10．判断方程$\left\{\begin{array}{l}{x=sinθ+\frac{1}{sinθ}}\\{y=sinθ-\frac{1}{sinθ}}\end{array}\right.$（θ是参数且θ∈（0，π））表示的曲线的形状．
20．已知等差数列{an}的公差d为整数，且ak=k2+2，a2k=（k+2）2，其中k为常数且k∈N*
（1）求k及an
（2）设a1＞1，{an}的前n项和为Sn，等比数列{bn}的首项为l，公比为q（q＞0），前n项和为Tn，若存在正整数m，使得$\frac{{S}_{2}}{{S}_{m}}={T}_{3}$，求q．
7．设O是坐标原点，若直线l：y=x+b（b＞0）与圆x2+y2=4交于不同的两点P1、P2，且$|{\overrightarrow{{P_1}{P_2}}}|≥|{\overrightarrow{O{P_1}}+\overrightarrow{O{P_2}}}|$，则实数b的最大值是（　　）
A．$\sqrt{2}$B．2C．$\sqrt{6}$D．$2\sqrt{2}$
4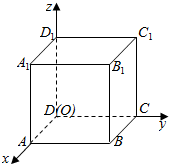．以正方体ABCD-A1B1C1D1的顶点D为坐标原点O，如图建立空间直角坐标系，则与$\overrightarrow{D{B_1}}$共线的向量的坐标可以是（　　）
A．（2，-2，2）B．（-2，-2，2）C．（-2，2，2）D．（-2，-2，-2）
5．用更相减损术法，计算56和264的最大公约数时，需要做的减法次数是（　　）
A．5、B．6C．7D．8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网