题目内容
9.生产甲乙两种精密电子产品,用以下两种方案分别生产出甲乙产品共3件,现对这两种方案生产的产品分别随机调查了100次,得到如下统计表:①生产2件甲产品和1件乙产品
| 正次品 | 甲正品 甲正品 乙正品 | 甲正品 甲正品 乙次品 | 甲正品 甲次品 乙正品 | 甲正品 甲次品 乙次品 | 甲次品 甲次品 乙正品 | 甲次品 甲次品 乙次品 |
| 频 数 | 15 | 20 | 16 | 31 | 10 | 8 |
| 正次品 | 乙正品 乙正品 甲正品 | 乙正品 乙正品 甲次品 | 乙正品 乙次品 甲正品 | 乙正品 乙次品 甲次品 | 乙次品 乙次品 甲正品 | 乙次品 乙次品 甲次品 |
| 频 数 | 8 | 10 | 20 | 22 | 20 | 20 |
(1)按方案①生产2件甲产品和1件乙产品,求这3件产品平均利润的估计值;
(2)从方案①②中选其一,生产甲乙产品共3件,欲使3件产品所得总利润大于30元的机会多,应选用哪个?
分析 (1)由题意求出按方案①生产2件甲产品和1件乙产品的利润表,由此能求出这3件产品平均利润的估计值.
(2)方案①生产的2件甲产品和1件乙产品所得总利润大于30元的情形有70,45,求出其频率;方案②生产1件甲产品和2件乙产品所得总利润大于30元的情形有80,55,35,求出其频率,由此能求出结果.
解答 解:(1)由题意得按方案①生产2件甲产品和1件乙产品的利润表为:
| 利润 | 70 | 25 | 45 | 0 | 20 | -25 |
| 频率 | 0.15 | 0.20 | 0.16 | 0.31 | 0.10 | 0.08 |
70×0.15+25×0.20+45×0.16+0×0.31+20×0.10+(-25)×0.08=22.70.
(2)方案①生产的2件甲产品和1件乙产品所得总利润大于30元的情形有70,45,
频率是:0.15+0.16=0.31,
方案②生产1件甲产品和2件乙产品所得总利润大于30元的情形有80,55,35,
频率是:0.08+0.10+0.20=0.38,
∵0.38>0.31,
∴选择方案②.
点评 本题考查频率率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.

练习册系列答案
相关题目
4.执行如图所示的程序框图,若输入的k,b,r的值分别为2,2,4,则输出i的值是( )
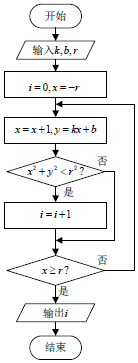

| A. | 4 | B. | 3 | C. | 6 | D. | 7 |
1.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的离心率为2,则该双曲线的渐近线方程为( )
| A. | x±y=0 | B. | $x±\sqrt{3}y=0$ | C. | $\sqrt{3}x±y=0$ | D. | 2x±y=0 |
18.如图所示,在△ABC内随机选取一点P,则△PBC的面积不超过△ABC面积一半的概率是( )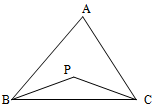

| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
19.$\frac{{{i^{2017}}}}{1-2i}$=( )
| A. | $-\frac{2}{5}+\frac{1}{5}i$ | B. | $\frac{2}{5}-\frac{1}{5}i$ | C. | $\frac{2}{5}+\frac{1}{5}i$ | D. | $-\frac{2}{5}-\frac{1}{5}i$ |