题目内容
1.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的离心率为2,则该双曲线的渐近线方程为( )| A. | x±y=0 | B. | $x±\sqrt{3}y=0$ | C. | $\sqrt{3}x±y=0$ | D. | 2x±y=0 |
分析 根据题意,得双曲线的渐近线方程为y=±$\frac{b}{a}$x.再由双曲线离心率为2,得到c=2a,由定义知b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$a,代入即得此双曲线的渐近线方程.
解答 解:∵双曲线的方程是$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0),
∴双曲线渐近线为y=±$\frac{b}{a}$x.
又∵离心率为e=$\frac{c}{a}$=2,
∴c=2a,
∴b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$a,
由此可得双曲线渐近线为y=±$\frac{\sqrt{3}a}{a}$x=±$\sqrt{3}$x,即:
故答案为:$\sqrt{3}x±y=0$.
故选:C.
点评 本题给出双曲线的离心率,求双曲线的渐近线方程,着重考查了双曲线的标准方程与基本概念,属于基础题.

练习册系列答案
相关题目
9.生产甲乙两种精密电子产品,用以下两种方案分别生产出甲乙产品共3件,现对这两种方案生产的产品分别随机调查了100次,得到如下统计表:
①生产2件甲产品和1件乙产品
②生产1件甲产品和2件乙产品
已知生产电子产品甲1件,若为正品可盈利20元,若为次品则亏损5元;生产电子产品乙1件,若为正品可盈利30元,若为次品则亏损15元.
(1)按方案①生产2件甲产品和1件乙产品,求这3件产品平均利润的估计值;
(2)从方案①②中选其一,生产甲乙产品共3件,欲使3件产品所得总利润大于30元的机会多,应选用哪个?
①生产2件甲产品和1件乙产品
| 正次品 | 甲正品 甲正品 乙正品 | 甲正品 甲正品 乙次品 | 甲正品 甲次品 乙正品 | 甲正品 甲次品 乙次品 | 甲次品 甲次品 乙正品 | 甲次品 甲次品 乙次品 |
| 频 数 | 15 | 20 | 16 | 31 | 10 | 8 |
| 正次品 | 乙正品 乙正品 甲正品 | 乙正品 乙正品 甲次品 | 乙正品 乙次品 甲正品 | 乙正品 乙次品 甲次品 | 乙次品 乙次品 甲正品 | 乙次品 乙次品 甲次品 |
| 频 数 | 8 | 10 | 20 | 22 | 20 | 20 |
(1)按方案①生产2件甲产品和1件乙产品,求这3件产品平均利润的估计值;
(2)从方案①②中选其一,生产甲乙产品共3件,欲使3件产品所得总利润大于30元的机会多,应选用哪个?
6.2017年3月27日,一则“清华大学要求从2017级学生开始,游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响.游泳作为一项重要的求生技能和运动项目受到很多人的喜爱.其实,已有不少高校将游泳列为必修内容.某中学为了解2017届高三学生的性别和喜爱游泳是否有关,对100名高三学生进行了问卷调查,得到如下列联表:
已知在这100人中随机抽取1人,抽到喜欢游泳的学生的概率为$\frac{3}{5}$.
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.9%的把握认为喜欢游泳与性别有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| 喜欢游泳 | 不喜欢游泳 | 合计 | |
| 男生 | 10 | ||
| 女生 | 20 | ||
| 合计 |
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.9%的把握认为喜欢游泳与性别有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
13.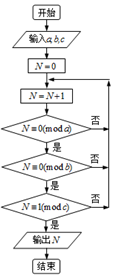 若正整数N除以正整数m后的余数为n,则记为N≡n(bmodm),例如10≡4(bmod6),如图程序框图的算法源于我国古代《孙子算经》中的“孙子定理”的某一环节,执行该框图,输入a=2,b=3,c=5,则输出的N=( )
若正整数N除以正整数m后的余数为n,则记为N≡n(bmodm),例如10≡4(bmod6),如图程序框图的算法源于我国古代《孙子算经》中的“孙子定理”的某一环节,执行该框图,输入a=2,b=3,c=5,则输出的N=( )
 若正整数N除以正整数m后的余数为n,则记为N≡n(bmodm),例如10≡4(bmod6),如图程序框图的算法源于我国古代《孙子算经》中的“孙子定理”的某一环节,执行该框图,输入a=2,b=3,c=5,则输出的N=( )
若正整数N除以正整数m后的余数为n,则记为N≡n(bmodm),例如10≡4(bmod6),如图程序框图的算法源于我国古代《孙子算经》中的“孙子定理”的某一环节,执行该框图,输入a=2,b=3,c=5,则输出的N=( )| A. | 6 | B. | 9 | C. | 12 | D. | 21 |
11.已知点M(x,y)为平面区域D:$\left\{\begin{array}{l}{x-y≥0}\\{y-\frac{1}{x}≤0}\\{y≥a,(0<a<1)}\end{array}\right.$内的一个动点,若z=$\frac{y+1}{x}$的最大值为3,则区域D的面积为( )
| A. | ln2+$\frac{5}{8}$ | B. | ln2-$\frac{1}{2}$ | C. | ln2+$\frac{1}{8}$ | D. | ln2-$\frac{3}{8}$ |
 已知四棱锥的正视图与俯视图如图所示,该四棱锥的体积为24,则四棱锥的侧视图面积为6,四棱锥的表面积为60.
已知四棱锥的正视图与俯视图如图所示,该四棱锥的体积为24,则四棱锥的侧视图面积为6,四棱锥的表面积为60.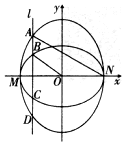 如图,已知椭圆C1的中心在原点O,长轴左、右端点M、N在x轴上,椭圆C2的短轴为MN,且C1、C2的离心率都为e,直线l⊥MN,l与C1交于两点,与C2交于两点,这四点纵坐标从大到小依次为A、B、C、D.
如图,已知椭圆C1的中心在原点O,长轴左、右端点M、N在x轴上,椭圆C2的短轴为MN,且C1、C2的离心率都为e,直线l⊥MN,l与C1交于两点,与C2交于两点,这四点纵坐标从大到小依次为A、B、C、D.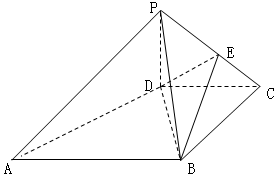 如图,在四棱锥P-ABCD中,底面ABCD是梯形,AB∥CD,PD⊥平面ABCD,BD⊥DC,PD=BD=DC=$\frac{1}{2}$AB,E为PC中点.
如图,在四棱锥P-ABCD中,底面ABCD是梯形,AB∥CD,PD⊥平面ABCD,BD⊥DC,PD=BD=DC=$\frac{1}{2}$AB,E为PC中点.