题目内容
在圆O中,长度为
的弦AB不过圆心,则
•
的值为 .
| 2 |
| AO |
| AB |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:取AB的中点为C,可得OC⊥AB,可得
•
=(
+
)•2
=2
2+2
•
,由数量积的运算可得.
| AO |
| AB |
| AC |
| CO |
| AC |
| AC |
| CO |
| AC |
解答:
解:取AB的中点为C,由圆的性质可得OC⊥AB,
∴
•
=(
+
)•2
=2
2+2
•
=2×(
)2+0
=1
故答案为:1

∴
| AO |
| AB |
| AC |
| CO |
| AC |
=2
| AC |
| CO |
| AC |
=2×(
| ||
| 2 |
=1
故答案为:1

点评:本题考查平面向量数量积的运算,涉及向量的加减运算和转化的思想,属基础题.

练习册系列答案
相关题目
假设在5秒内的任何时刻,两条不相关的短信机会均等地进人同一部手机,若这两条短信进人手机的时间之差小于2秒,手机就会受到干扰,则手机受到干扰的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知数列{an}满足an+1=an-
,且a1=5,设{an}的n项和为Sn,则使得Sn取得最大值的序号n的值为( )
| 5 |
| 7 |
| A、7 | B、8 | C、7或8 | D、8或9 |
 根据《环境空气质量指数AQI技术规定》,AQI共分为六级:(0,50]为优,(50,100]为良,(100,150]为轻度污染,(150,200]为中度污染,(200,300]为重度污染,300以上为严重污染.如图是根据盐城市2013年12月份中20天的AQI统计数据绘制的频率分布直方图.由图中的信息可以得出这20天中盐城市环境空气质量优或良的总天数为
根据《环境空气质量指数AQI技术规定》,AQI共分为六级:(0,50]为优,(50,100]为良,(100,150]为轻度污染,(150,200]为中度污染,(200,300]为重度污染,300以上为严重污染.如图是根据盐城市2013年12月份中20天的AQI统计数据绘制的频率分布直方图.由图中的信息可以得出这20天中盐城市环境空气质量优或良的总天数为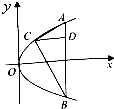 如图,直角三角形ABC的三个顶点在给定的抛物线y2=2px(p>0)上,斜边AB平行于y轴,则AB边上的高|CD|=
如图,直角三角形ABC的三个顶点在给定的抛物线y2=2px(p>0)上,斜边AB平行于y轴,则AB边上的高|CD|=