题目内容
20.已知{an}为等差数列,前n项和为Sn(n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.(Ⅰ)求{an}和{bn}的通项公式;
(Ⅱ)求数列{a2nbn}的前n项和(n∈N*).
分析 (Ⅰ)设等差数列{an}的公差为d,等比数列{bn}的公比为q.通过b2+b3=12,求出q,得到${b_n}={2^n}$.然后求出公差d,推出an=3n-2.
(Ⅱ)设数列{a2nbn}的前n项和为Tn,利用错位相减法,转化求解数列{a2nbn}的前n项和即可.
解答 (Ⅰ)解:设等差数列{an}的公差为d,等比数列{bn}的公比为q.由已知b2+b3=12,得${b_1}(q+{q^2})=12$,而b1=2,所以q2+q-6=0.又因为q>0,解得q=2.所以,${b_n}={2^n}$.
由b3=a4-2a1,可得3d-a1=8.
由S11=11b4,可得a1+5d=16,联立①②,解得a1=1,d=3,
由此可得an=3n-2.
所以,{an}的通项公式为an=3n-2,{bn}的通项公式为${b_n}={2^n}$.
(Ⅱ)解:设数列{a2nbn}的前n项和为Tn,由a2n=6n-2,有${T_n}=4×2+10×{2^2}+16×{2^3}+…+(6n-2)×{2^n}$,$2{T_n}=4×{2^2}+10×{2^3}+16×{2^4}+…+(6n-8)×{2^n}+(6n-2)×{2^{n+1}}$,
上述两式相减,得$-{T_n}=4×2+6×{2^2}+6×{2^3}+…+6×{2^n}-(6n-2)×{2^{n+1}}$=$\frac{{12×(1-{2^n})}}{1-2}-4-(6n-2)×{2^{n+1}}=-(3n-4){2^{n+2}}-16$.
得${T_n}=(3n-4){2^{n+2}}+16$.
所以,数列{a2nbn}的前n项和为(3n-4)2n+2+16.
点评 本题考查等差数列以及等比数列通项公式的求法,数列求和,考查转化思想以及计算能力.

 考前必练系列答案
考前必练系列答案| A. | (-1,2) | B. | (0,1) | C. | (-1,0) | D. | (1,2) |
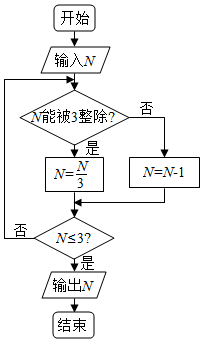 阅读右面的程序框图,运行相应的程序,若输入N的值为24,则输出N的值为( )
阅读右面的程序框图,运行相应的程序,若输入N的值为24,则输出N的值为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
| A. | [-2,2] | B. | $[-2\sqrt{3},2]$ | C. | $[-2,2\sqrt{3}]$ | D. | $[-2\sqrt{3},2\sqrt{3}]$ |
| X | -1 | 0 | 1 | 2 |
| Pk | $\frac{1}{8}$ | $\frac{1}{8}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| A. | 54000 | B. | 100400 | C. | 100600 | D. | 100800 |