题目内容

11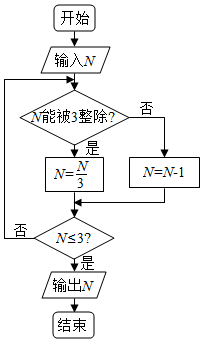．阅读右面的程序框图，运行相应的程序，若输入N的值为24，则输出N的值为（　　）
A．0B．1C．2D．3

分析 根据程序框图，进行模拟计算即可．

解答 解：第一次N=24，能被3整除，N=$\frac{24}{3}=8$≤3不成立，
第二次N=8，8不能被3整除，N=8-1=7，N=7≤3不成立，
第三次N=7，不能被3整除，N=7-1=6，N=$\frac{6}{3}$=2≤3成立，
输出N=2，
故选：C

点评 本题主要考查程序框图的识别和应用，根据条件进行模拟计算是解决本题的关键．

练习册系列答案
相关题目
1．已知a，b，c分别为△ABC三个内角A，B，C的对边，acosC+$\sqrt{3}$asinC-b-2c=0．
（1）求A．
（2）若等差数列{an}的公差不为零，且a1cosA=-1，且a2、a4、a8成等比数列，设{an}的前n项和为Tn，求数列{$\frac{1}{{T}_{n}}$}的前n项和Sn．
2．（1+$\frac{1}{x^2}$）（1+x）6展开式中x2的系数为（　　）
A．15B．20C．30D．35
19．已知（1+3x）n的展开式中含有x2的系数是54，则n=4．
6．已知函数f（x）=x2+2cosx，g（x）=ex（cosx-sinx+2x-2），其中e≈2.71828…是自然对数的底数．
（Ⅰ）求曲线y=f（x）在点（π，f（π））处的切线方程；
（Ⅱ）令h（x）=g （x）-a f（x）（a∈R），讨论h（x）的单调性并判断有无极值，有极值时求出极值．
16．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-x+3，x≤1}\\{x+\frac{2}{x}，x＞1}\end{array}$，设a∈R，若关于x的不等式f（x）≥|$\frac{x}{2}$+a|在R上恒成立，则a的取值范围是（　　）
A．[-$\frac{47}{16}$，2]B．[-$\frac{47}{16}$，$\frac{39}{16}$]C．[-2$\sqrt{3}$，2]D．[-2$\sqrt{3}$，$\frac{39}{16}$]
3．在△ABC中，内角A，B，C所对的边分别为a，b，c．已知a＞b，a=5，c=6，sinB=$\frac{3}{5}$．
（Ⅰ）求b和sinA的值；
（Ⅱ）求sin（2A+$\frac{π}{4}$）的值．
20．已知{an}为等差数列，前n项和为Sn（n∈N*），{bn}是首项为2的等比数列，且公比大于0，b2+b3=12，b3=a4-2a1，S11=11b4．
（Ⅰ）求{an}和{bn}的通项公式；
（Ⅱ）求数列{a2nbn}的前n项和（n∈N*）．
19．已知函数$f（x）=\left\{{\begin{array}{l}{{x^2}-x}\\{x+1}\end{array}}\right.，\begin{array}{l}{（x≥0）}\\{（x＜0）}\end{array}$，则f（2）=2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网