题目内容
20.正方体ABCD-A1B1C1D1中,M,N分别是棱BC,CC1上不与正方体顶点重合的动点,用平面AMN截正方体,下列关于截面的说法正确的有①②.①若BM=C1N,则截面为等腰梯形
②若BM=CM,且$CN>\frac{1}{2}C{C_1}$时,截面为五边形
③截面的面积存在最大值
④截面的面积存在最小值.
分析 画出正方体,根据动点M,N的不同位置动点不同 的截面;M,N分别是棱BC,CC1上不与正方体顶点重合的动点,考虑极限位置时 的截面形状以及面积极限判断.
解答 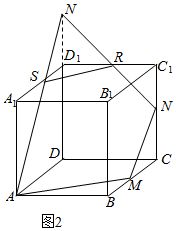
 解:对于①,如图1,若BM=C1N,
解:对于①,如图1,若BM=C1N,
则MN∥AD1,D1N=AM,截面AMND1为等腰梯形,故①正确;
对于②,如图2,若BM=CM,且$CN>\frac{1}{2}C{C_1}$时,
设截面与棱C1D1的交点为R,
延长DD1,使DD1∩NR=N1,连接AN1交A1D1于S,连接SR,
可证AN∥PQ,由△NRD1∽△QRC1,
可得C1R:D1R=C1N:D1N1,截面为五边形故②正确;
对于③,当BM=C1N→0时,过点A,M,N的截面→矩形,其面积接近最大,
∵M,N分别是棱BC,CC1上不与正方体顶点重合的动点,
∴BM=C1N≠0,∴截面的面积不存在最大值,故③错误;
对于④,当BM→BC时CN→0时,截面→等边三角形,边长为→$\sqrt{2}$,面积→$\frac{\sqrt{3}}{2}$,又M,N分别是棱BC,CC1上不与正方体顶点重合的动点,所以截面面积不存在最小值;故④错误;
故答案为:①②
点评 本题考查了正方体中线线关系以及截面形状问题;关键是考查空间想象能力;属于中档题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
8. 如图,A,B,C是一个无盖的正方体盒子展开后的平面图上的散点,则在正方体盒子中∠ABC=( )
如图,A,B,C是一个无盖的正方体盒子展开后的平面图上的散点,则在正方体盒子中∠ABC=( )
 如图,A,B,C是一个无盖的正方体盒子展开后的平面图上的散点,则在正方体盒子中∠ABC=( )
如图,A,B,C是一个无盖的正方体盒子展开后的平面图上的散点,则在正方体盒子中∠ABC=( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
5.函数f(x)的导函数f′(x),满足关系式f(x)=x2+2xf′(2)-lnx,则f(1)的值为( )
| A. | -2 | B. | -4 | C. | -6 | D. | -8 |
12.设集合A={x|x2-4x+3<0},B={x|2x-3>0},则A∩B=( )
| A. | (-3,-$\frac{3}{2}$) | B. | ($\frac{3}{2}$,3) | C. | (1,$\frac{3}{2}$) | D. | (-3,$\frac{3}{2}$) |
9.下表提供了某厂生产某产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据,
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,
(2)根据(1)中求出的线性回归方程,预测生产20吨该产品的生产能耗是多少吨标准煤?
附:回归直线的斜率和截距的最小二乘估计分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| x | 2 | 4 | 6 | 8 | 10 |
| y | 4 | 5 | 7 | 9 | 10 |
(2)根据(1)中求出的线性回归方程,预测生产20吨该产品的生产能耗是多少吨标准煤?
附:回归直线的斜率和截距的最小二乘估计分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
 甲、乙两名运动员的5次测试成绩如图所示,以这5次测试成绩为判断依据,则甲、乙两名运动员成绩稳定性较差的是甲.(填“甲、乙”)
甲、乙两名运动员的5次测试成绩如图所示,以这5次测试成绩为判断依据,则甲、乙两名运动员成绩稳定性较差的是甲.(填“甲、乙”)