题目内容
已知曲线C的参数方程为
(0<θ<2π),则点M(-1,
),N(1,
),P(2,2),Q(
,1)中,在曲线C上的点有( )
|
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:将参数方程的上式两边平方,应用同角三角函数的基本关系式化简,结合参数方程的第二式,得到普通方程,注意x,y的范围,即可判断M,N,P,Q是否在曲线C上.
解答:
解:曲线C的参数方程为
(0<θ<2π),
x2=(cos
+sin
)2=1+2sin
cos
=1+sinθ,
又2y=1+sinθ,
故曲线C的普通方程为x2=2y(0≤x≤
,0≤y≤1),
故点M(-1,
),N(1,
),P(2,2),Q(
,1)中N,Q在曲线上,M,P不在,
故选C.
|
x2=(cos
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
又2y=1+sinθ,
故曲线C的普通方程为x2=2y(0≤x≤
| 2 |
故点M(-1,
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
故选C.
点评:本题主要考查参数方程与普通方程的互化,注意x,y的范围,是一道基础题.

练习册系列答案
相关题目
函数f(x)=e-x•
则( )
| x |
A、仅有最小值
| ||||
B、仅有最大值
| ||||
C、既有最小值0,也有最大值
| ||||
| D、既无最大值,也无最小值 |
下列向量中不是单位向量的是( )
| A、(-1,0) | ||||||||
| B、(1,1) | ||||||||
| C、(cosa,sina) | ||||||||
D、
|
在△ABC中,已知2acosB=c,|
+
|=|
-
|,则△ABC为( )
| CA |
| CB |
| CA |
| CB |
| A、等边三角形 |
| B、等腰直角三角形 |
| C、锐角非等边三角形 |
| D、钝角三角形 |
当m<0时,复数2+m•i在复平面内对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
某校要求每位学生从7门课程中选修4门,其中甲、乙两门课程不能都选,则不同的选课方案有( )
| A、35种 | B、16种 |
| C、20种 | D、25种 |
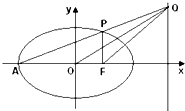 如图,在平面直角坐标系xOy中,已知A,F分别为椭圆C:
如图,在平面直角坐标系xOy中,已知A,F分别为椭圆C: