题目内容
当m＜0时，复数2+m•i在复平面内对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：由复数得到其对应点的坐标，结合m＜0可得答案．
解答：
解：复数2+m•i在复平面内对应的点的坐标为（2，m），
∵m＜0，
∴复数2+m•i在复平面内对应的点（2，m）位于第四象限．
故选：D．
∵m＜0，
∴复数2+m•i在复平面内对应的点（2，m）位于第四象限．
故选：D．
点评：本题考查了复数的代数表示法及其几何意义，是基础题．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知曲线C的参数方程为
（0＜θ＜2π），则点M（-1，
），N（1，
），P（2，2），Q（
，1）中，在曲线C上的点有（ ）
|
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
集合A={3，log2a}，B={a，b}，若A∩B={2}，则A∪B=（ ）
| A、{2，3，4} |
| B、{2，4} |
| C、{2，3} |
| D、{1，2，3，4} |
若
+（1+
i）2=a+bi（a，b∈R），则a+b=（ ）
| 1+i |
| i |
| 3 |
A、2
| ||
B、-2
| ||
C、2+2
| ||
D、2
|
已知x与y成线性相关，其统计数据如下表：
则x与y的线性回归方程
=
x+
必过点（ ）
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
| ? |
| y |
| ? |
| b |
| ? |
| a |
| A、（2，2） |
| B、（1.5，4） |
| C、（1.5，0） |
| D、（1，2） |
下列结论正确的是（ ）
①函数关系是一种确定性关系；
②在回归分析中，残差图中的纵坐标为残差；
③回归分析是对具有函数关系的两个变量进行统计分析的一种方法；
④复数-1+i的共轭复数是-1-i．
①函数关系是一种确定性关系；
②在回归分析中，残差图中的纵坐标为残差；
③回归分析是对具有函数关系的两个变量进行统计分析的一种方法；
④复数-1+i的共轭复数是-1-i．
| A、①② | B、①②③ |
| C、①②④ | D、①②③④ |
如图所示为一简谐振动的图象，则下列判断正确的是（ ）
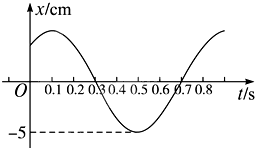
| A、该质点的振动周期为0.7s |
| B、该质点的振幅为5cm |
| C、该质点在0.1s和0.5s时振动速度最大 |
| D、该质点在0.3s和0.7s时的加速度为零 |
已知sinα=
，则cos4α的值是（ ）
| ||
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|