题目内容
曲线的ρ=sinθ-3cosθ直角坐标方程为 ．
考点：简单曲线的极坐标方程
专题：计算题,坐标系和参数方程
分析：运用x=ρcosθ，y=ρsinθ，ρ2=x2+y2即可化为直角坐标方程．
解答：
解：曲线ρ=sinθ-3cosθ，两边乘ρ，
则ρ2=ρsinθ-3ρcosθ，
则有x2+y2=y-3x，
即x2+y2+3x-y=0．
故答案为：x2+y2+3x-y=0．
则ρ2=ρsinθ-3ρcosθ，
则有x2+y2=y-3x，
即x2+y2+3x-y=0．
故答案为：x2+y2+3x-y=0．
点评：本题主要考查极坐标方程与直角坐标方程的互化，属于基础题．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
相关题目
算法流程图（如图所示）的运行结果为已知曲线C的参数方程为
（0＜θ＜2π），则点M（-1，
），N（1，
），P（2，2），Q（
，1）中，在曲线C上的点有（ ）
|
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
集合A={3，log2a}，B={a，b}，若A∩B={2}，则A∪B=（ ）
| A、{2，3，4} |
| B、{2，4} |
| C、{2，3} |
| D、{1，2，3，4} |
如图所示为一简谐振动的图象，则下列判断正确的是（ ）
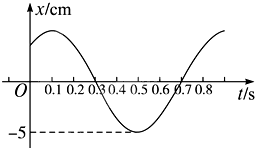
| A、该质点的振动周期为0.7s |
| B、该质点的振幅为5cm |
| C、该质点在0.1s和0.5s时振动速度最大 |
| D、该质点在0.3s和0.7s时的加速度为零 |