题目内容
【题目】已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标方程是ρ=asinθ,直线l的参数方程是 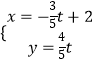 (t为参数)
(t为参数)
(1)若a=2,直线l与x轴的交点是M,N是圆C上一动点,求|MN|的最大值;
(2)直线l被圆C截得的弦长等于圆C的半径的 ![]() 倍,求a的值.
倍,求a的值.
【答案】
(1)解:当a=2时,圆C的直角坐标方程为x2+y2=2y,即x2+(y﹣1)2=1.∴圆C的圆心坐标为C(0,1),半径r=1.
令y= ![]() =0得t=0,把t=0代入x=﹣
=0得t=0,把t=0代入x=﹣ ![]() 得x=2.∴M(2,0).
得x=2.∴M(2,0).
∴|MC|= ![]() =
= ![]() .∴|MN|的最大值为|MC|+r=
.∴|MN|的最大值为|MC|+r= ![]()
(2)解:由ρ=asinθ得ρ2=aρsinθ,∴圆C的直角坐标方程是x2+y2=ay,即x2+(y﹣ ![]() )2=
)2= ![]() .
.
∴圆C的圆心为C(0, ![]() ),半径为|
),半径为| ![]() |,
|,
直线l的普通方程为4x+3y﹣8=0.
∵直线l被圆C截得的弦长等于圆C的半径的 ![]() 倍,
倍,
∴圆心C到直线l的距离为圆C半径的一半.
∴ ![]() =|
=| ![]() |,解得a=32或a=
|,解得a=32或a= ![]()
【解析】(1)求出圆C的圆心和半径,M点坐标,则|MN|的最大值为|MC|+r;(2)由垂径定理可知圆心到直线l的距离为半径的 ![]() ,列出方程解出.
,列出方程解出.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


