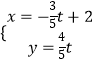题目内容
【题目】已知椭圆
的焦距为
，且过点
.
（Ⅰ）求椭圆
的方程；
（Ⅱ）设
为椭圆上一点，过点
作
轴的垂线，垂足为
.取点
，连接
，过点
作的垂线交轴于点
.点
是点关于
轴的对称点，作直线
，问这样作出的直线是否与椭圆一定有唯一的公共点？并说明理由.
【答案】(1) 
.
(2) 直线
与椭圆只有一个公共点；理由见解析.
【解析】（1）因为椭圆过点
且
椭圆C的方程是
（2）
由题意，各点的坐标如上图所示，
则的直线方程：
化简得
又
，
所以
带入
求得最后
所以直线与椭圆只有一个公共点.
第（1）题根据题意确定
的大小，再将带入方程，确定椭圆的方程；第（2）题是存在性问题，根据题意，设出
，根据条件写出的直线方程，并进行化简，然而
点坐标又在椭圆上，带入方程，求出，即可判断直线是否与椭圆C一定有唯一的公共点.
练习册系列答案
相关题目
【题目】微信红包是一款年轻人非常喜欢的手机应用.某网络运营商对甲、乙两个品牌各
种型号的手机在相同环境下抢到红包的个数进行统计，得到如下数据：
品牌 型号 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
甲品牌（个） | 4 | 3 | 8 | 6 | 12 |
乙品牌（个） | 5 | 7 | 9 | 4 | 3 |
红包个数 手机品牌 | 优良 | 一般 | 合计 |
甲品牌（个） | |||
乙品牌（个） | |||
合计 |
（Ⅰ）如果抢到红包个数超过个的手机型号为“优良”，否则为“一般”，请完成上述表格，并据此判断是否有
的把握认为抢到红包的个数与手机品牌有关？
（Ⅱ）不考虑其它因素，现要从甲、乙两品牌的种型号中各选出
种型号的手机进行促销活动，求恰有一种型号是“优良”，另一种型号是“一般”的概率；
参考公式：随机变量
的观察值计算公式：
，
其中
.临界值表：
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
