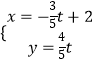题目内容
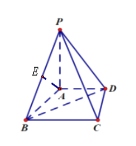
【题目】如图,在四棱锥![]() 中,
中,![]() ,侧面
,侧面![]() 底面
底面![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,且二面角
,且二面角![]() 等于
等于![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由![]() 得,
得,![]() ,由侧面
,由侧面![]() 底面
底面![]() 得
得![]() 侧面
侧面![]() ,由面面垂直的判定即可证明;(2)由
,由面面垂直的判定即可证明;(2)由![]() 侧面
侧面![]() ,可得
,可得![]() , 得
, 得![]() 是二面角
是二面角![]() 的平面角,
的平面角,![]() ,推得
,推得![]() 为等腰直角三角形,取
为等腰直角三角形,取![]() 的中点
的中点![]() ,连接
,连接![]() 可得
可得![]() ,由平面
,由平面![]() 平面
平面![]() ,得
,得![]() 平面
平面![]() ,证明
,证明![]() 平面
平面![]() ,得点
,得点![]() 到平面
到平面![]() 的距离
的距离![]() 等于点
等于点![]() 到平面
到平面![]() 的距离,
的距离,![]() ,再利用
,再利用![]() 求解即可
求解即可
(1)证明:由![]() 可得,
可得,![]()
因为侧面![]() 底面
底面![]() ,交线为
,交线为![]()
![]() 底面
底面![]() 且
且![]()
则![]() 侧面
侧面![]() ,
,![]() 平面
平面![]()
所以,平面![]() 平面
平面![]() ;
;
(2)由![]() 侧面
侧面![]() 可得,
可得,![]() ,
,
则![]() 是二面角
是二面角![]() 的平面角,
的平面角,![]()
由![]() 可得,
可得,![]() 为等腰直角三角形
为等腰直角三角形
取![]() 的中点
的中点![]() ,连接
,连接![]() 可得
可得![]()
因为平面![]() 平面
平面![]() ,交线为
,交线为![]() 平面
平面![]() 且
且![]()
所以![]() 平面
平面![]() ,点
,点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
因为![]() 平面
平面![]()
则![]() 平面
平面![]()
所以点![]() 到平面
到平面![]() 的距离
的距离![]() 等于点
等于点![]() 到平面
到平面![]() 的距离,
的距离,![]() .
.
设![]() ,则
,则![]()
在![]() 中,
中,![]() ;在
;在![]() 中,
中,![]()
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]()
即![]()
所以,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】为了解学生暑假阅读名著的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表.
|
|
|
|
| |
男生 |
|
|
|
|
|
女生 |
|
|
|
|
|
(![]() )从这班学生中任选一名男生,一名女生,求这两名学生阅读名著本数之和为
)从这班学生中任选一名男生,一名女生,求这两名学生阅读名著本数之和为![]() 的概率?
的概率?
(![]() )若从阅读名著不少于
)若从阅读名著不少于![]() 本的学生中任选
本的学生中任选![]() 人,设选到的男学生人数为
人,设选到的男学生人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
(![]() )试判断男学生阅读名著本数的方差
)试判断男学生阅读名著本数的方差![]() 与女学生阅读名著本数的方程
与女学生阅读名著本数的方程![]() 的大小.
的大小.