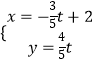题目内容
【题目】在平面直角坐标系xOy中，角α与角β均以Ox为始边，它们的终边关于y轴对称，若sinα= 
，则cos（α﹣β）= ．
【答案】﹣ 
【解析】解：方法一：∵角α与角β均以Ox为始边，它们的终边关于y轴对称，
∴sinα=sinβ= 
，cosα=﹣cosβ，
∴cos（α﹣β）=cosαcosβ+sinαsinβ=﹣cos2α+sin2α=2sin2α﹣1= 
﹣1=﹣
方法二：∵sinα= ，
当α在第一象限时，cosα= 
，
∵α，β角的终边关于y轴对称，
∴β在第二象限时，sinβ=sinα= ，cosβ=﹣cosα=﹣ ，
∴cos（α﹣β）=cosαcosβ+sinαsinβ=﹣ × + × =﹣
：∵sinα= ，
当α在第二象限时，cosα=﹣ ，
∵α，β角的终边关于y轴对称，
∴β在第一象限时，sinβ=sinα= ，cosβ=﹣cosα= ，
∴cos（α﹣β）=cosαcosβ+sinαsinβ=﹣ × + × =﹣
综上所述cos（α﹣β）=﹣ ，
所以答案是：﹣
【考点精析】掌握同角三角函数基本关系的运用和两角和与差的余弦公式是解答本题的根本，需要知道同角三角函数的基本关系：
；
;（3） 倒数关系：
；两角和与差的余弦公式：
．
【题目】某届奥运会上，中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二，某校体育爱好者在高三年级一班至六班进行了“本届奥运会中国队表现”的满意度调查
结果只有“满意”和“不满意”两种
，从被调查的学生中随机抽取了50人，具体的调查结果如表：
班号 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
频数 | 5 | 9 | 11 | 9 | 7 | 9 |
满意人数 | 4 | 7 | 8 | 5 | 6 | 6 |
（1）在高三年级全体学生中随机抽取一名学生，由以上统计数据估计该生持满意态度的概率；
（2）若从一班至二班的调查对象中随机选取4人进行追踪调查，记选中的4人中对“本届奥运会中国队表现”不满意的人数为
，求随机变量的分布列及数学期望．
【题目】针对国家提出的延迟退休方案，某机构进行了网上调查，所有参与调查的人中，持“支持”、“保留”和“不支持”态度的人数如下表所示：
支持 | 保留 | 不支持 | |
|
|
|
|
|
|
|
|
(1)在所有参与调查的人中，用分层抽样的方法抽取
个人，已知从持“不支持”态度的人中抽取了
人，求的值；
(2)在接受调查的人中，有
人给这项活动打出的分数如下：
，
，
，
，
，
，
，
，
，
，把这个人打出的分数看作一个总体，从中任取一个数，求该数与总体平均数之差的绝对值超过
的概率．
