题目内容

设多项式1-x+x2-x3+…-x17可以写成a0+a1y+a2y2+…a17y17，其中y=x+1，则a2=
 
．
考点：二项式定理的应用
专题：二项式定理
分析：根据题意，a2是二项式（1+y）17的展开式中y2的系数，利用二项展开式系数求解．
解答： 解：由题意，x=y-1，则多项式1-x+x2-x3+…-x17，变形为多项式1-（y-1）+（y-1）2-（y-1）3+…-（y-1）17，a2是此多项式展开式中y2的系数，为
C
0
2
+
C
1
3
+
C
2
4
+…
C
2
17
=
C
3
18
=
18×17×16
6
=816
故答案为816．
点评：本题考查二项展开式的系数的求法．
练习册系列答案
相关题目
已知点P（2，5），M为圆（x+1）2+（y-1）2=4上任一点，则PM的最大值为
 
．
已知圆P：x2+y2=4y及抛物线S：x2=8y，过圆心P作直线l，此直线与上述两曲线的四个交点，自左向右顺次记为A，B，C，D，如果线段AB，BC，CD的长按此顺序构成一个等差数列，则直线l的斜率为
 
．
已知F1，F2是双曲线3x2-5y2=15的两个焦点，点A在双曲线上，且△F1AF2面积等于2
2
，则∠F1AF2=
 
．
已知半径为l的球，若以其一条半径为正方体的一条棱作正方体，则此正方体内部的球面面积为
 
．
若（
x
+
1
x
）n的二项展开式中第5项是常数项，则正整数n的值是
 
．
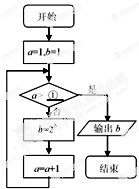已知流程图如图（a=1，b=1下分别是a＞①，b=2b，a=+1）所示，该程序运行后，为使输出的b值为16，则循环体的判断框内①处应填的是（　　）
A、2B、3C、4D、16
设
e1
，
e2
是夹角为
2π
3
的单位向量，且
a
=2
e1
+3
e2
，
b
=k
e1
-4
e2
．若
a
⊥
b
，则实数k的值为（　　）
A、
16
7
B、
32
7
C、16
D、32
在△AB中，已知
BC
•
CA
=
CA
•
AB
，若|
BA
+
BC
|=2，且B∈[
π
3
，
2π
3
]，则
BA
•
BC
的取值范围为（　　）
A、[-2，
2
3
]
B、[-1，
2
3
]
C、[0，
2
3
]
D、[1，
2
3
]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网