题目内容
4.已知实数x,y满足条件$\left\{\begin{array}{l}x-y≥-1\\ x+y≤4\\ x-2y≤0\end{array}\right.$,若存在实数a使得函数z=ax+y(a<0)取到最大值z(a)的解有无数个,则a=-1,z(a)=1.分析 z=ax+y可化为y=-ax+z,由题意作平面区域,从而利用数形结合求解.
解答 解:z=ax+y可化为y=-ax+z,
由题意作平面区域如下,
结合图象可知,
y=-ax+z与直线y=x+1重合,
故-a=1,z=1,
故答案为:-1,1.
点评 本题考查了学生的作图能力及数形结合的思想方法的应用,属于中档题.

练习册系列答案
相关题目
12.已知复数z=$\frac{|2\sqrt{3}-2i|+bi}{1-i}$(b∈R)的实部比虚部小6,则复数z-bi在复平面上对应点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.执行如图所示的程序框图,如果输入的变量t∈[0,3],则输出的S属于( )


| A. | [0,7] | B. | [0,4] | C. | [1,7] | D. | [1,4] |
16.执行如图所示的程序框图,如果输入的t=50,则输出的n=( )
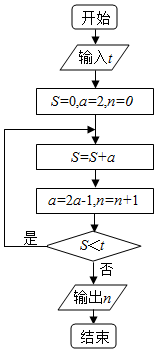

| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
