题目内容
函数f（x）=Asin（ωx+φ）（A＞0，|φ|＜
）的图象相邻两个对称中心间距离为π，且f（x）有一条对称轴是x=
，则函数y=f（
-x）是（ ）
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| A、偶函数且在x=0处取最小值 |
| B、偶函数且在x=0处取最大值 |
| C、奇函数且在x=0处取最大值 |
| D、奇函数且在x=0处取最小值 |
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：根据条件求出函数的周期，利用周期性和对称轴求出函数f（x）的解析式即可得到结论．
解答：
解：∵函数f（x）=Asin（ωx+φ）（A＞0，|φ|＜
）的图象相邻两个对称中心间距离为π，
即函数的周期满足
=π，即T=2π=
，
解得ω=1，即f（x）=Asin（x+φ），
则函数的对称轴为x+φ=kπ+
，
∵f（x）有一条对称轴是x=
，
∴
+φ=kπ+
，即φ=kπ+
，
∵|φ|＜
，∴当k=0时，φ=
，
则f（x）=Asin（x+
），
则函数y=f（
-x）=Asin（
-x+
）=Asin（
-x）=Acosx，为偶函数，
∵A＞0，∴在x=0处取最大值，
故选：B
| π |
| 2 |
即函数的周期满足
| T |
| 2 |
| 2π |
| ω |
解得ω=1，即f（x）=Asin（x+φ），
则函数的对称轴为x+φ=kπ+
| π |
| 2 |
∵f（x）有一条对称轴是x=
| π |
| 4 |
∴
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
∵|φ|＜
| π |
| 2 |
| π |
| 4 |
则f（x）=Asin（x+
| π |
| 4 |
则函数y=f（
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
∵A＞0，∴在x=0处取最大值，
故选：B
点评：本题主要考查三角函数解析式的求法，利用三角函数的性质求出函数的解析式是解决本题的关键．
练习册系列答案
相关题目
已知f（x）=x+
，则f（x）为（ ）
| 1 |
| x |
| A、既是奇函数又是偶函数 |
| B、非奇非偶函数 |
| C、奇函数 |
| D、偶函数 |
已知椭圆
+x2=1与抛物线x2=ay有相同的焦点F，O为原点，点P是抛物线准线上一动点，点A在抛物线上，且|AF|=4，则|PA|+|PO|的最小值为（ ）
| y2 |
| 5 |
A、2
| ||
B、4
| ||
C、3
| ||
D、4
|
函数f（x）=
+
的定义域是（ ）
| x+3 |
| 1 |
| x+2 |
| A、{x|x≠2} |
| B、{x|x≥-3} |
| C、{x|x≥-3或x≠-2} |
| D、{x|x≥-3且x≠-2} |
在四面体ABCD中，∠ABC=∠ABD=∠ADC=
，则下列是直角的为（ ）
| π |
| 2 |
| A、∠BCD | B、∠BDC |
| C、∠CBD | D、∠ACD |
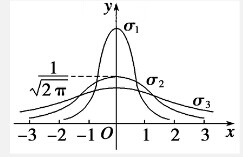如图，当σ取三个不同的值σ1，σ2，σ3的三种正态曲线N（0，σ2）的图象，那么σ1，σ2，σ3的大小关系是（ ）| A、σ1＞1＞σ2＞σ3＞0 |
| B、0＜σ1＜σ2＜1＜σ3 |
| C、σ1＞σ2＞1＞σ3＞0 |
| D、0＜σ1＜σ2=1＜σ3 |
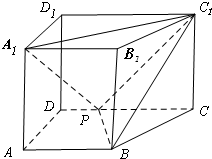如图，直四棱柱ABCD-A1B1C1D1底面ABCD直角梯形，AB∥CD，∠BAD=90°，P是棱CD上一点，AB=2，AD=