题目内容
观察下题的解答过程：
已知正实数a，b满足a+b=1，求
+
的最大值
解：∵
•
≤
=a+
，
•
≤
=b+
相加得
•
+
•
=
（
+
）≤a+b+3=4∴
+
≤2
，等号在a=b=
时取得，即
+
的最大值为2
请类比上题解法，使用综合法证明下题：
已知正实数x，y，z满足x+y+z=2，求证：
+
+
≤
．
已知正实数a，b满足a+b=1，求
| 2a+1 |
| 2b+1 |
解：∵
| 2a+1 |
| 2 |
| ||||
| 2 |
| 3 |
| 2 |
| 2b+1 |
| 2 |
| ||||
| 2 |
| 3 |
| 2 |
相加得
| 2a+1 |
| 2 |
| 2b+1 |
| 2 |
| 2 |
| 2a+1 |
| 2b+1 |
| 2b+1 |
| 2b+1 |
| 2 |
| 1 |
| 2 |
| 2a+1 |
| 2b+1 |
| 2 |
请类比上题解法，使用综合法证明下题：
已知正实数x，y，z满足x+y+z=2，求证：
| 2x+1 |
| 2y+1 |
| 2z+1 |
| 21 |
考点：综合法与分析法(选修）
专题：选作题,综合法
分析：利用基本不等式，结合类比思想，再相加，即可证明结论．
解答：
解：∵
•
≤
=x+
，
•
≤
=y+
，
•
≤
=z+
…（7分）
相加得(
+
+
)•
≤x+y+z+5=7
即
+
+
≤7•
=
，等号在x=y=z=
时取得．…（13分）
| 2x+1 |
|
| ||||||
| 2 |
| 5 |
| 3 |
| 2y+1 |
|
| ||||||
| 2 |
| 5 |
| 3 |
| 2z+1 |
|
| ||||||
| 2 |
| 5 |
| 3 |
相加得(
| 2x+1 |
| 2y+1 |
| 2z+1 |
|
即
| 2x+1 |
| 2y+1 |
| 2z+1 |
| ||
|
| 21 |
| 2 |
| 3 |
点评：本题考查类比思想，同时给出一个最值的求法，比较新颖．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
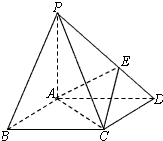如图，在底面是菱形的四棱锥P-ABCD中，∠ABC=60°，PA=AC=1，PB=PD=
甲、乙两位学生参加数学竞赛培训，如图所示茎叶图的数据是他们在培训期间五次预赛的成绩．已知甲、乙两位学生的平均分相同．