题目内容
设S1=12，S2=12+22+12，S3=12+22+32+22+12，…，Sn=12+22+32+…+n2+…+22+12，用数学归纳法证明“Sn=
”的过程中，第二步从k到k+1左边应添加的项为 ．
| n(2n+1) |
| 3 |
考点：数学归纳法
专题：证明题,点列、递归数列与数学归纳法
分析：ak=12+22+…+k2+…+22+12，ak+1=12+22+…+k2+（k+1）2+k2+…+22+12，即可得出结论．
解答：
解：当n=k时，Sk=12+22+32+…+k2+…+22+12，
当n=k+1时，Sk+1=12+22+32+…+k2+（k+1）2+k2+…+22+12，
故从k到k+1应添加的项为（k+1）2+k2．
故答案为：（k+1）2+k2．
当n=k+1时，Sk+1=12+22+32+…+k2+（k+1）2+k2+…+22+12，
故从k到k+1应添加的项为（k+1）2+k2．
故答案为：（k+1）2+k2．
点评：本题考查数学归纳法的运用，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
在下列给出的四个命题中，为真命题的是（ ）
| A、?a∈R，?b∈Q，a2+b2=0 |
| B、?n∈Z，?m∈Z，nm=m |
| C、?n∈Z，?m∈Z，n＞m2 |
| D、?a∈R，?b∈Q，a2+b2=1 |
若点P到直线y=-2的距离比它到点A（0，1）的距离大1，则点P的轨迹为（ ）
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
要得到y=2sin（2x+
）的图象，只需将y=2sinx的图象上的所有的点（ ）
| π |
| 6 |
A、向左平移
| ||||
B、向右平移
| ||||
C、横坐标缩短到原来的
| ||||
D、横坐标缩短到原来的
|
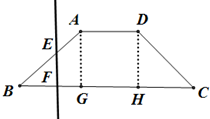如图，已知底角为45°的等腰梯形ABCD，底边BC长为5cm，腰长为2