题目内容

19．在（x+a）5（其中a≠0）的展开式中，x2的系数与x3的系数相同，则a的值为（　　）
A．-2B．-1C．1D．2

分析 通过二项式定理，写出（x+a）5（其中a≠0）的展开式中通项Tk+1=${C}_{5}^{k}$x5-kak，利用x2的系数与x3的系数相同可得到关于a的方程，进而计算可得结论．

解答 解：在（x+a）5（其中a≠0）的展开式中，通项Tk+1=${C}_{5}^{k}$x5-kak，
∵x2的系数与x3的系数相同，
∴${C}_{5}^{3}$a3=${C}_{5}^{2}$a2，
又∵a≠0，
∴a=1，
故选：C．

点评 本题考查二项式系数的性质，注意区分系数与二项式系数这两个概念，注意解题方法的积累，属于中档题．

练习册系列答案
相关题目
9．某中学从高三甲、乙两个班中各选出7名学生参加数学竞赛，他们取得的成绩如下：
甲班：92，80，79，78，85，96，85
乙班：81，91，91，76，81，92，83
（Ⅰ）若竞赛成绩在90分以上的视为“优秀生”，则从“优秀生”中任意选出2名，乙班恰好只有1名的概率是多少？
（Ⅱ）根据两组数据完成两班数学竞赛成绩的茎叶图，指出甲班学生成绩的众数，乙班学生成绩中位数，并请你利用所学的平均数、方差的知识分析一下两个班学生的竞赛成绩情况．
10．已知F1，F2分别为椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，Q为椭圆C上的一点，且△QF1O（O为坐标原点）为正三角形，若射线QF1，QO与椭圆分别相交于点P，R，则△QF1O与△QPR的面积的比值为$\frac{\sqrt{3}+1}{8}$．
7．已知集合A={2n|n∈N，n＜5}，B={0，1，2，…，9，10}，则集合∁BA中元素的个数为（　　）
A．5B．6C．7D．8
14．设集合A={x|x2+x-6＜0}，B={x|x＜0}，则A∩∁RB=（　　）
A．{x|0≤x＜2}B．{x|-3＜x＜2}C．{x|-6＜x＜0}D．{x|x≥0}
4．在正三棱柱ABC-A1B1C1中，AB=$\sqrt{2}$AA1，求证：BC1=AB1．
11．某种汽车在水泥路面上的刹车距离（刹车距离指汽车刹车后由于惯性往前滑行的距离）y m和汽车车速x km/h有如下关系：y=$\frac{1}{20}$x+$\frac{1}{180}$x2．
（I）在一次交通事故中，测得这种汽车的刹车距离不小于$\frac{81}{2}$m，求这辆汽车刹车前的车速的最小值；
（Ⅱ）定义刹车摩擦比值：在刹车过程中，刹车距离（m）与10倍“车重（吨）”求和后，再除以车速（km/h）所得的比值为刹车摩擦比值．若这辆汽车的车重为2吨，求这辆汽车的最小刹车摩擦比值及此时的车速．
8．执行如图所示的程序框图，输出k的值为（　　）
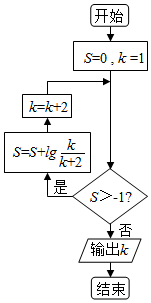
A．10B．11C．12D．13
9．某程序的框图如图所示，执行该程序，若输入的N=5，则输出i=（　　）
A．6B．7C．8D．9

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网