题目内容
13．求经过直线2x+y-3=0与3x+2y-1=0的交点，圆心为（2，-3）的圆的方程．分析 联立直线方程求得两直线的交点坐标，进一步求出圆的半径，代入圆的标准方程得答案．
解答 解：联立$\left\{\begin{array}{l}{2x+y-3=0}\\{3x+2y-1=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=5}\\{y=-7}\end{array}\right.$，
∴两直线的交点为（5，-7），
则所求圆的半径为r=$\sqrt{（5-2）^{2}+（-7+3）^{2}}=5$．
∴所求圆的方程为（x-2）2+（y+3）2=25．
点评 本题考查圆的标准方程，训练了方程组的解法，是基础题．
练习册系列答案
相关题目
4．已知向量$\overrightarrow{a}$=（2，-1），$\overrightarrow{b}$=（1，7），则下列结论正确的是（ ）
| A． | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | B． | $\overrightarrow{a}$∥$\overrightarrow{b}$ | C． | $\overrightarrow{a}$⊥（$\overrightarrow{a}$+$\overrightarrow{b}$） | D． | $\overrightarrow{a}$⊥（$\overrightarrow{a}$-$\overrightarrow{b}$） |
5．已知|$\overrightarrow{a}$|=5，|$\overrightarrow{b}$|=4，$\overrightarrow{a}$•$\overrightarrow{b}$=-10，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{2π}{3}$ | C． | $\frac{π}{6}$ | D． | $\frac{5π}{6}$ |
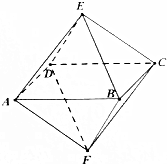如图，已知一个八面体的各条棱长均为1，四边形ABCD为正方形，给出下列命题：