题目内容
8.连续两次抛掷一枚骰子,记录向上的点数,则向上的点数之差的绝对值为3的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{3}$ |
分析 先求出基本事件总数n=6×6=36,再求出向上的点数之差的绝对值为3包含的基本事件个数,由此能求出向上的点数之差的绝对值为3的概率.
解答 解:连续两次抛掷一枚骰子,记录向上的点数,
基本事件总数n=6×6=36,
向上的点数之差的绝对值为3包含的基本事件有:
(1,4),(4,1),(2,5),(5,2),(3,6),(6,3),共6个,
∴向上的点数之差的绝对值为3的概率p=$\frac{6}{36}=\frac{1}{6}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
19.已知直线l:kx-y-3=0与圆O:x2+y2=4交于A、B两点且$\overrightarrow{OA}$•$\overrightarrow{OB}$=2,则k=( )
| A. | 2 | B. | ±$\sqrt{2}$ | C. | ±2 | D. | $\sqrt{2}$ |
3.某渔业公司为了解投资收益情况,调查了旗下的养鱼场和远洋捕捞队近10个月的利润情况.根据所收集的数据得知,近10个月总投资养鱼场一千万元,获得的月利润频数分布表如下:
近10个月总投资远洋捕捞队一千万元,获得的月利润频率分布直方图如下:
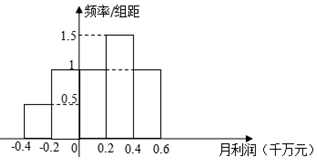
(Ⅰ)根据上述数据,分别计算近10个月养鱼场与远洋捕捞队的月平均利润;
(Ⅱ)公司计划用不超过6千万元的资金投资于养鱼场和远洋捕捞队,假设投资养鱼
场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元,且投资养鱼场的资金不少于投资远洋捕捞队的资金的2倍.试用调查数据,给出公司分配投资金额的建议,使得公司投资这两个项目的月平均利润之和最大.
| 月利润(单位:千万元) | -0.2 | -0.1 | 0 | 0.1 | 0.3 |
| 频数 | 2 | 1 | 2 | 4 | 1 |

(Ⅰ)根据上述数据,分别计算近10个月养鱼场与远洋捕捞队的月平均利润;
(Ⅱ)公司计划用不超过6千万元的资金投资于养鱼场和远洋捕捞队,假设投资养鱼
场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元,且投资养鱼场的资金不少于投资远洋捕捞队的资金的2倍.试用调查数据,给出公司分配投资金额的建议,使得公司投资这两个项目的月平均利润之和最大.
17.设不等式组$\left\{\begin{array}{l}{y≤x+1}\\{2x+y≤7}\\{x+2y≥5}\end{array}\right.$,表示的平面区域为D,若D中存在点在曲线y=ax2上,则实数a的取值范围是( )
| A. | [1,2] | B. | [$\frac{1}{3}$,3] | C. | [$\frac{1}{6}$,2] | D. | [$\frac{1}{9}$,2] |