题目内容
3.设集合A={x|x2-3x+2≤0},B={(x,y)|x∈A,y∈A},则A∩B=( )| A. | A | B. | B | C. | A∪B | D. | ∅ |
分析 求解一元二次不等式化简集合A,可知A是数集,集合B是点集,则A∩B是空集.
解答 解:集合A={x|x2-3x+2≤0}={x|1≤x≤2},
B={(x,y)|x∈A,y∈A}={(x,y)|$\left\{\begin{array}{l}{1≤x≤2}\\{1≤y≤2}\end{array}\right.$},
∵A为数集,B为点集,
∴A∩B=∅.
故选:D.
点评 本题考查了集合的定义与运算问题,是基础题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
18.下表是某校高三一次月考5个班级的数学、物理的平均成绩:
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量x,y的线性回归方程$\hat y=\hat bx+\hat a$;
(Ⅱ)从以上5个班级中任选两个参加某项活动,求至少有一个班级数学平均分在115分以上的概率.
附:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
| 班级 | 1 | 2 | 3 | 4 | 5 |
| 数学(x分) | 111 | 113 | 119 | 125 | 127 |
| 物理(y分) | 92 | 93 | 96 | 99 | 100 |
(Ⅱ)从以上5个班级中任选两个参加某项活动,求至少有一个班级数学平均分在115分以上的概率.
附:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
12. 某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为A、B、C三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为A、B、C三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
 某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为A、B、C三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为A、B、C三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).| 工种类别 | A | B | C |
| 赔付频率 | $\frac{1}{1{0}^{5}}$ | $\frac{2}{1{0}^{5}}$ | $\frac{1}{1{0}^{4}}$ |
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
13.执行如图所示的程序框图,则输出的k=( )
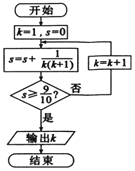

| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
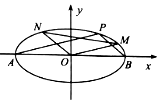 已知A,B分别为椭圆C:$\frac{x^2}{4}+\frac{y^2}{2}=1$的左、右顶点,P为椭圆C上异于A,B两点的任意一点,直线PA,PB的斜率分别记为k1,k2.
已知A,B分别为椭圆C:$\frac{x^2}{4}+\frac{y^2}{2}=1$的左、右顶点,P为椭圆C上异于A,B两点的任意一点,直线PA,PB的斜率分别记为k1,k2.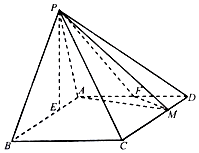 在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,AD=2$\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.
在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,AD=2$\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.