题目内容
20.已知函数f(x)=ex(x2+x+a)在(0,f(0))处的切线与直线2x-y-3=0平行,其中a∈R.(1)求a的值;
(2)求函数f(x)在区间[-2,2]上的最值.
分析 (1)求出函数的导数,计算f′(0)=2,求出a的值即可;
(2)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最值即可.
解答 解:(1)f′(x)=ex(x2+3x+a+1),
故f′(0)=a+1,而切线的斜率是2,
故a+1=2,解得:a=1;
(2)由(1)得f(x)=ex(x2+x+1),
f′(x)=ex(x+1)(x+2),
令f′(x)>0,解得:x>-1或x<-2,
令f′(x)<0,解得:-2<x<-1,
故函数f(x)在[-2,-1)递减,在(-1,2]递增,
而f(-2)=$\frac{3}{{e}^{3}}$,f(-1)=$\frac{1}{e}$,f(2)=7e2,
故f(x)在[-2,2]的最小值是$\frac{1}{e}$,最大值是7e2.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及切线的意义,是一道中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
11.某著名纺织集团为了减轻生产成本继续走高的压力,计划提高某种产品的价格,为此销售部在10月1日至10月5日连续五天对某个大型批发市场中该产品一天的销售量及其价格进行了调查,其中该产品的价格x(元)与销售量y(万件)之间的数据如表所示:
已知销售量y与价格x之间具有线性相关关系,其回归直线方程为:$\widehat{y}$=-3.2x+$\widehat{a}$,若该集团提高价格后该批发市场的日销售量为7.36万件,则该产品的价格约为( )
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 |
| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(万件) | 11 | 10 | 8 | 6 | 5 |
| A. | 14.2元 | B. | 10.8元 | C. | 14.8元 | D. | 10.2元 |
8.已知抛物线C:y2=2px(p>0)的焦点为F,P是C上一点,过P点作C的切线l交x轴于Q点,且Q在C的准线上,则△PFQ一定是( )
| A. | 等边三角形 | B. | 等腰直角三角形 | ||
| C. | 直角三角形但不是等腰三角形 | D. | 等腰三角形但不是直角三角形 |
5.与双曲线$C:\frac{x^2}{16}-\frac{y^2}{9}=1$有相同的渐近线的双曲线E的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$或$\frac{5}{4}$ | D. | $\frac{5}{3}$或$\frac{5}{3}$ |
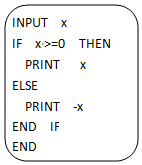 当输入的x 值为-5时,如图的程序运行的结果等于5.
当输入的x 值为-5时,如图的程序运行的结果等于5.