题目内容

15．已知集合A={x||x-2|≤1}，且A∩B=∅，则集合B可能是（　　）
A．{2，5}B．{x|x2≤1}C．（1，2）D．（-∞，-1）

分析 根据交集的运算即可求出．

解答 解：∵集合A={x||x-2|≤1}=[1，3]，由A∩B=∅，
则B⊆（-∞，1）∪（3，+∞），
故选：D

点评 本题考查了集合的交集的运算，属于基础题．

练习册系列答案
相关题目
5．与双曲线$C：\frac{x^2}{16}-\frac{y^2}{9}=1$有相同的渐近线的双曲线E的离心率为（　　）
A．$\frac{5}{3}$B．$\frac{5}{4}$C．$\frac{5}{3}$或$\frac{5}{4}$D．$\frac{5}{3}$或$\frac{5}{3}$
6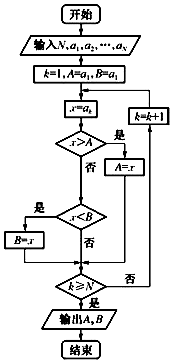．如果执行如图所示的程序框图，输入正整数N（N≥2）和实数a1，a2，…，aN，输出A，B，则（　　）
A．A+B为a1，a2，…，aN的和
B．A和B分别是a1，a2，…，aN中最大的数和最小的数
C．$\frac{A+B}{2}$为a1，a2，…，aN的算术平均数
D．A和B分别是a1，a2，…，aN中最小的数和最大的数
3．已知f（x）是奇函数，当x＞0时，f（x）=1gx，设a=f（3），b=$f（\frac{1}{4}）$，c=f（-2），则（　　）
A．a＞c＞bB．a＞b＞cC．c＞a＞bD．b＞a＞c
10．在锐角△ABC中，内角A，B，C的对边分别是a，b，c且$1+\frac{{\sqrt{3}}}{3}sin2A=2{sin^2}\frac{B+C}{2}$．
（I）求A；
（II）若△ABC的外接圆半径为$2\sqrt{3}$，求△ABC面积的最大值．
20．已知数列{an}的前n项和为Sn，且${S_n}={a_n}+{n^2}-1（{n∈{N^*}}）$．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）定义x=[x]+＜x＞，其中[x]为实数x的整数部分，＜x＞为x的小数部分，且0≤＜x＞＜1，记cn=＜$\frac{{{a_n}{a_{n+1}}}}{S_n}$＞，求数列{cn}的前n项和Tn．
7．已知$f（x）=\left\{{\begin{array}{l}{f（x+1），}&{x＜2}\\{{2^x}，}&{x≥2}\end{array}}\right.$，则f（log23）=（　　）
A．12B．6C．4D．2
4．设数列{an}的前n项和为Sn，已知a2=2，an+2+（-1）n-1an=1，则S40=（　　）
A．260B．250C．240D．230
5．实数x、y满足$\left\{\begin{array}{l}{x≤3}\\{x+y≥0}\\{x-y+6≥0}\end{array}\right.$，若z=ax+y的最大值为3a+9，最小值为3a-3，则a的取值范围是[-1，1]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网