题目内容
4.函数f(x)=k•ax-a-x(a>0且a≠1)是定义域为R的奇函数.(Ⅰ)求k的值;
(Ⅱ)讨论不等式f(x2+x)+f(2x-4)<0的解集;
(Ⅲ)若$f(1)=\frac{8}{3}$,且g(x)=a2x+a-2x-2m•f(x)+2在[1,+∞)恒为正,求实数m的取值范围.
分析 (Ⅰ)根据奇函数的定义求解即可;
( II)根据奇函数的性质,不等式可转化为f(x2+x)<f(4-2x),对a进行分类讨论,由函数的单调性分别求解即可;
(III)由f(1)=$\frac{8}{3}$,求出a=3,不等式可转化为32x+3-2x-2m•(3x-3-x)+2>0恒成立,构造函数令t=3x-3-x,t>$\frac{8}{3}$,得出2m<t+$\frac{4}{t}$,只需求出右式的最小值即可.
解答 解:(Ⅰ)由函数f(x)为R上的奇函数,
则f(0)=0,得k-1=0,解得k=1;
( II)由(Ⅰ)得:f(x)=ax-a-x,
不等式f(x2+x)+f(2x-4)<0,
即f(x2+x)<f(4-2x)
当a>1时,f(x)递增,故x2+x<4-2x,
解得:-4<x<1,
故不等式的解集是(-4,1);
当1>a>0时,f(x)递减,故x2+x>4-2x,
解得:x>1或x<-4,
故不等式的解集是:(-∞,-4)∪(1,+∞);
(III)又∵f(1)=$\frac{8}{3}$,即a-a-1=$\frac{8}{3}$,解得a=-$\frac{1}{3}$(舍去)或a=3,
∴f(x)=3x-3-x,
g(x)=a2x+a-2x-2m•f(x)+2在[1,+∞)恒为正,
∴32x+3-2x-2m•(3x-3-x)+2>0恒成立,
令t=3x-3-x,则t≥$\frac{8}{3}$,
∴2m<t+$\frac{4}{t}$,
显然可知t+$\frac{4}{t}$的最小值为$\frac{25}{6}$,
∴$m∈(-∞,\frac{25}{12})$.
点评 本题考查了奇函数的概念和应用,利用构造函数的方法把恒成立问题转化为求函数最值问题.

练习册系列答案
相关题目
5.已知函数f(x)=$\frac{1}{3}$x3-mx2+x+2有两个极值点,则m的取值范围是( )
| A. | (-1,1) | B. | [-1,1] | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-1)∪(1,+∞) |
9.下列函数中,在区间(0,+∞)上为增函数的是( )
| A. | y=lg(x+1) | B. | y=tanx | C. | y=2-x | D. | y=x-2 |
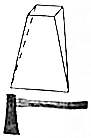 斧头的形状叫楔形,在《算数书》中又称之为“郓(y$\stackrel{、}{u}$n)都”或“壍(qi$\stackrel{、}{a}$n)堵”:其上底是一矩形,下底是一线段.有一斧头:上厚为三,下厚为六,高为五及袤(m$\stackrel{、}{a}$o)为二,问此斧头的体积为几何?意思就是说有一斧头形的几何体,上底为矩形,下底为一线段,上底的长为3,下底线段长为6,上下底间的距离(高)为5,上底矩形的宽为2,则此几何体的体积是( )
斧头的形状叫楔形,在《算数书》中又称之为“郓(y$\stackrel{、}{u}$n)都”或“壍(qi$\stackrel{、}{a}$n)堵”:其上底是一矩形,下底是一线段.有一斧头:上厚为三,下厚为六,高为五及袤(m$\stackrel{、}{a}$o)为二,问此斧头的体积为几何?意思就是说有一斧头形的几何体,上底为矩形,下底为一线段,上底的长为3,下底线段长为6,上下底间的距离(高)为5,上底矩形的宽为2,则此几何体的体积是( )