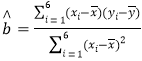题目内容
【题目】已知抛物线y2＝2px（p＞0）的焦点为F，点A（2，y0）为抛物线上一点，且|AF|＝4．
（1）求抛物线的方程；
（2）直线l：y＝x+m与抛物线交于不同两点P，Q，若
，其中O为坐标原点，求m的值．
【答案】（1）y2＝8x； （2）﹣11.
【解析】
（1）由抛物线的定义到焦点的距离，转化为到准线的距离求出
的值，即可求出抛物线方程；
（2）直线与抛物线联立，由根与系数的关系，由向量数量积即可求出
的值．
（1）已知抛物线y2＝2px（p＞0）过点A（2，y0），
且|AF|＝4则
，
∴p＝4，
故抛物线的方程为y2＝8x；
（2）设P（x1，y1），Q（x2，y2），
联立 
，得x2+（2m﹣8）x+m2＝0，
△＝（2m﹣8）2﹣4m2＞0，得m＜2，
∴x1+x2＝8﹣2m，
，
，
∴m＝﹣11或m＝3，
∵m＜2，∴m＝﹣11．
练习册系列答案
相关题目
【题目】研究机构对某校学生往返校时间的统计资料表明：该校学生居住地到学校的距离
（单位：千米）和学生花费在上学路上的时间
（单位：分钟）有如下的统计资料：
到学校的距离 | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
花费的时间 | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果统计资料表明与有线性相关关系，试求：
（1）判断与是否有很强的线性相关性？
（相关系数
的绝对值大于0.75时，认为两个变量有很强的线性相关性，精确到0.01）
（2）求线性回归方程
（精确到0.01）；
（3）将
分钟的时间数据
称为美丽数据，现从这6个时间数据中任取2个，求抽取的2个数据全部为美丽数据的概率.
参考数据：
，
，
，
，
，
参考公式：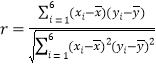
，
