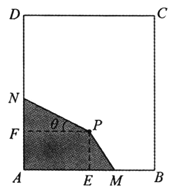
题目内容
【题目】设函数![]() 分别在
分别在![]() 、
、![]() 处取得极小值、极大值.
处取得极小值、极大值.![]() 平面上点
平面上点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,该平面上动点
,该平面上动点![]() 满足
满足![]() ,点
,点![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点.
的对称点.
(Ⅰ)求点![]() 、
、![]() 的坐标;
的坐标;
(Ⅱ)求动点![]() 的轨迹方程.
的轨迹方程.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
(Ⅰ)先对函数求导,得到![]() ,解对应方程
,解对应方程![]() ,判断函数单调性,从而可求出函数在
,判断函数单调性,从而可求出函数在![]() 处取得极小值,在
处取得极小值,在![]() 取得极大值,进而可求出结果;
取得极大值,进而可求出结果;
(Ⅱ)设![]() ,
,![]() ,得到
,得到![]() ,
,![]() 的坐标,根据
的坐标,根据![]() ,得到
,得到![]() ,再由题意,得到
,再由题意,得到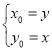 代入
代入![]() ,化简整理,即可得出结果.
,化简整理,即可得出结果.
(Ⅰ)因为![]() ,所以
,所以![]() ,
,
令![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以,函数在![]() 处取得极小值,在
处取得极小值,在![]() 取得极大值,
取得极大值,
故![]() ,
,![]() ,又
,又![]() ,
,![]() ;
;
![]() 点
点![]() ,
,![]() ;
;
(Ⅱ)设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ①
①
又![]() 点
点![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点
的对称点
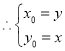 代入①得:
代入①得:![]() ,即为
,即为![]() 的轨迹方程.
的轨迹方程.

练习册系列答案
相关题目