题目内容
4.点A,B分别为圆M:x2+(y-3)2=1与圆N:(x-3)2+(y-8)2=4上的动点,点C在直线x+y=0上运动,则|AC|+|BC|的最小值为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 根据题意,算出圆M关于直线l对称的圆M'方程为(x+3)2+y2=1.当点P位于线段NM'上时,线段AB的长就是|AC|+|BC|的最小值,由此结合对称的知识与两点间的距离公式加以计算,即可得出|AC|+|BC|的最小值.
解答  解:设圆C'是圆M:x2+(y-3)2=1关于直线x+y=0对称的圆
解:设圆C'是圆M:x2+(y-3)2=1关于直线x+y=0对称的圆
可得M'(-3,0),圆M'方程为(x+3)2+y2=1,
可得当点P位于线段NM'上时,线段AB长是圆N与圆M'上两个动点之间的距离最小值,
此时|AC|+|BC|的最小值为AB,
N(3,8),圆的半径R=2,
∵|NM'|=$\sqrt{(-3-3)^{2}+{8}^{2}}$=$\sqrt{36+64}=\sqrt{100}$=10,
可得|AB|=|NM'|-R-r=10-2-1=7
因此|AC|+|BC|的最小值为7,
故选:A.
点评 本题给出直线l与两个定圆,求圆上两个点A、B与直线l上动点P的距离之和的最小值,着重考查了直线的方程、圆的方程和直线与圆的位置关系等知识,属于中档题.

练习册系列答案
相关题目
15.已知复数z满足z•i=1+i(i是虚数单位),则复数z的共轭复数在复平面内所对应的点的坐标为( )
| A. | (1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (-1,1) |
19.已知f(x)=$\left\{\begin{array}{l}{(3a-1)x+4a,x<1}\\{-x+1,x≥1}\end{array}\right.$是定义在R上的减函数,则实数a的取值范围是( )
| A. | [$\frac{1}{7}$,+∞) | B. | [$\frac{1}{7}$,$\frac{1}{3}$) | C. | (-∞,$\frac{1}{3}$) | D. | (-∞,$\frac{1}{7}$]∪($\frac{1}{3}$,+∞) |
9. 若正整数N除以正整数m后的余数为n,则记为N≡n(mod m),例如10≡4(mod 6).下面程序框图的算法源于我国古代闻名中外的(中国剩余定理),执行该程序框图,则输出的n等于( )
若正整数N除以正整数m后的余数为n,则记为N≡n(mod m),例如10≡4(mod 6).下面程序框图的算法源于我国古代闻名中外的(中国剩余定理),执行该程序框图,则输出的n等于( )
 若正整数N除以正整数m后的余数为n,则记为N≡n(mod m),例如10≡4(mod 6).下面程序框图的算法源于我国古代闻名中外的(中国剩余定理),执行该程序框图,则输出的n等于( )
若正整数N除以正整数m后的余数为n,则记为N≡n(mod m),例如10≡4(mod 6).下面程序框图的算法源于我国古代闻名中外的(中国剩余定理),执行该程序框图,则输出的n等于( )| A. | 17 | B. | 16 | C. | 15 | D. | 13 |
16. 在四棱锥P-ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,PA⊥底面ABCD,E是棱PD上异于P,D的动点.设$\frac{PE}{ED}$=m,则“0<m<2”是三棱锥C-ABE的体积不小于1的( )
在四棱锥P-ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,PA⊥底面ABCD,E是棱PD上异于P,D的动点.设$\frac{PE}{ED}$=m,则“0<m<2”是三棱锥C-ABE的体积不小于1的( )
 在四棱锥P-ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,PA⊥底面ABCD,E是棱PD上异于P,D的动点.设$\frac{PE}{ED}$=m,则“0<m<2”是三棱锥C-ABE的体积不小于1的( )
在四棱锥P-ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,PA⊥底面ABCD,E是棱PD上异于P,D的动点.设$\frac{PE}{ED}$=m,则“0<m<2”是三棱锥C-ABE的体积不小于1的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.运行如图程序框图,则当输出y的值最大时,输入的x值等于( )
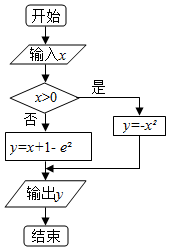

| A. | 0 | B. | 1 | C. | -1 | D. | 2 |