题目内容

13．设实数a，b满足0≤a，b≤8，且b2=16+a2，则b-a的最大值为4．

分析 由题意可知b2=16+a2，为焦点在y轴上的双曲线，设目标函数b-a=t，则当目标函数经过点A（0，4），t的值最大，问题得以解决．

解答 解：b2=16+a2，
即为$\frac{{b}^{2}}{16}$-$\frac{{a}^{2}}{16}$=1，
∴顶点坐标为（0，4），
设目标函数b-a=t，
则当目标函数经过点A（0，4），t的值最大，
即t=b-a=4，
故b-a的最大值为4，
故答案为：4．

点评 本题考查了双曲线的定义，以及目标函数的最值问题，属于基础题．

练习册系列答案
相关题目
3．设f（x）=$\left\{\begin{array}{l}{4{x}^{3}+6{x}^{2}+2（x≤0）}\\{2{e}^{ax}（x＞0）}\end{array}\right.$在区间[-2，2]上最大值为4，则实数a的取值范围为（　　）
A．[$\frac{1}{2}$ln2，+∞]B．[0，$\frac{1}{2}$ln2]C．（-∞，0]D．（-∞，$\frac{1}{2}$ln2]
4．点A，B分别为圆M：x2+（y-3）2=1与圆N：（x-3）2+（y-8）2=4上的动点，点C在直线x+y=0上运动，则|AC|+|BC|的最小值为（　　）
A．7B．8C．9D．10
1．函数f（x）=$\left\{\begin{array}{l}{{x}^{3}，x≤0}\\{lg（x+1），x＞0}\end{array}\right.$若f（2x）＞f（x2-3），则实数x的取值范围是（　　）
A．（-1，3）B．（-∞，-1）∪（3，+∞）C．（-∞，-3）∪（1，+∞）D．（-3，1）
8．在梯形ABCD中，AB∥CD，AB=2CD，E为BC中点，若$\overrightarrow{AE}=x\overrightarrow{AB}+y\overrightarrow{AD}$，则x+y=$\frac{5}{4}$．
18．己知f（x）=ex，g（x）=x．
（1）求y=f（x）•g（x）在x=1处的切线方程；
（2）试比较ef（x-2）＞与g（x）的大小，并证明．
5．已知曲线C的方程是mx2+ny2=1（m＞0mn＞0），且曲线C过A（$\frac{\sqrt{2}}{4}$，$\frac{\sqrt{2}}{2}$），B（$\frac{\sqrt{6}}{6}$，$\frac{\sqrt{3}}{3}$）两点，O为坐标原点
（Ⅰ）求曲线C的方程；
（Ⅱ）设M（x1，y1），N（x2，y2）是曲线C上两点，且OM⊥ON，求证：直线MN恒与一个定圆相切．
2．已知数列{sinan}是公比为-1的等比数列，若数列{an}是等差数列，则其公差可能是（　　）
A．-$\frac{3π}{2}$B．-$\frac{π}{2}$C．πD．2π
3．运行如图所示的程序框图后，输出的m值是（　　）
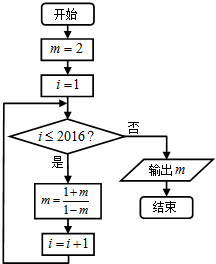
A．-3B．$-\frac{1}{2}$C．$\frac{1}{3}$D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网