题目内容
5.已知函数f(x)=cosx+ax2-1,a∈R,若对于任意的实数x恒有f(x)≥0,则实数a的取值范围是( )| A. | [$\frac{1}{2}$,+∞) | B. | ($\frac{1}{2}$,+∞) | C. | [-$\frac{1}{4}$,+∞) | D. | ($\frac{1}{4}$,+∞) |
分析 对于任意的实数x恒有f(x)≥0,即有cosx+ax2-1≥0,即ax2≥1-cosx≥0,显然a≥0,运用参数分离和二倍角公式可得2a≥($\frac{sin\frac{x}{2}}{\frac{x}{2}}$)2,求出右边函数的范围,即可得到a的范围.
解答 解:对于任意的实数x恒有f(x)≥0,即有cosx+ax2-1≥0,
即ax2≥1-cosx≥0,显然a≥0,
x=0时,显然成立;由偶函数的性质,只要考虑x>0的情况.
当x>0时,a≥$\frac{1-cosx}{{x}^{2}}$=$\frac{2si{n}^{2}\frac{x}{2}}{{x}^{2}}$,
即为2a≥($\frac{sin\frac{x}{2}}{\frac{x}{2}}$)2,
由x>0,则$\frac{x}{2}$=t>0,考虑sint-t的导数为cost-1≤0,
即sint-t递减,即有sint-t<0,即sint<t,
则有$\frac{sint}{t}$<1,故($\frac{sin\frac{x}{2}}{\frac{x}{2}}$)2<1,
即有2a≥1,解得a≥$\frac{1}{2}$.
则实数a的取值范围为[$\frac{1}{2}$,+∞).
故选:A.
点评 本题考查不等式恒成立问题的解法,注意运用分类讨论的思想方法和转化思想,考查导数的运用:判断单调性,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.方程[x]=x+a有解([x]表示不大于x的最大整数),则参数a的取值集合是( )
| A. | {a|0≤a<1} | B. | {a|-1<a≤0} | C. | {a|-1<a<1} | D. | {a|a∈R,a∉Z} |
10.设等差数列{an}的前n项和为Sn,若a1=1,S4=22,则S6=( )
| A. | 49 | B. | 51 | C. | 53 | D. | 55 |
17.直线l:x-y+1=0关于x轴对称的直线方程为( )
| A. | x+y-1=0 | B. | x-y+1=0 | C. | x+y+1=0 | D. | x-y-1=0 |
15.同时具有性质“周期为π,图象关于直线x=$\frac{π}{3}$对称,在$[-\frac{π}{6},\frac{π}{3}]$上是增函数”的函数是( )
| A. | $y=sin(\frac{x}{2}+\frac{π}{6})$ | B. | $y=cos(2x+\frac{π}{3})$ | C. | $y=cos(2x-\frac{π}{6})$ | D. | $y=sin(2x-\frac{π}{6})$ |
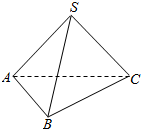 如图,在棱长都相等的四面体SABC中,给出如下三个命题:
如图,在棱长都相等的四面体SABC中,给出如下三个命题: