题目内容
已知椭圆Γ:
+
=1(a>b>0)的右焦点为F,椭圆的上顶点和两焦点连线构成等边三角形且面积为
.
(Ⅰ)求椭圆Γ的标准方程;
(Ⅱ)若直线l:x=my+q(m≠0)与椭圆Γ交于不同的两点A、B,设点A关于椭圆长轴的对称点为A1,试求A1、F、B三点共线的充要条件.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(Ⅰ)求椭圆Γ的标准方程;
(Ⅱ)若直线l:x=my+q(m≠0)与椭圆Γ交于不同的两点A、B,设点A关于椭圆长轴的对称点为A1,试求A1、F、B三点共线的充要条件.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意知a=2c,bc=
,由此能求出椭圆Γ的标准方程是
+
=1.
(2)联立
⇒(3m2+4)y2+6mqy+(3q2-12)=0,由此根的判别式、韦达定理结合已知条件推导出A1,F,B三点共线的充要条件是|m|>2且q=4.
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
(2)联立
|
解答:
解:(1)由题意知a=2c,bc=
,…(2分)
∴a=2,b=
,
椭圆Γ的标准方程是
+
=1.…(4分)
(2)联立
⇒(3m2+4)y2+6mqy+(3q2-12)=0…(5分)
由△=12[3m2q2-(3m2+4)(q2-4)]=48(3m2+4-q2)>0
得3m2+4-q2>0①…(7分)
记A(x1,y1),B(x2,y2),
则y1+y2=
,y1y2=
∵F(1,0),∴
=(x1-1,-y1),
=(x2-1,y2),
因A1,F,B三点共线,
∴(x1-1)y2-(x2-1)(-y1)=0…(10分)
∴(x1-1)y2-(x2-1)(-y1)=(my1+q-1)y2+(my2+q-1)y1
=2my1y2+(q-1)(y1+y2)
=2m•
+(q-1)•
=2m•
,②
解得q=4,m≠0.…(12分)
由①②知A1,F,B三点共线的充要条件是|m|>2且q=4.…(13分)
| 3 |
∴a=2,b=
| 3 |
椭圆Γ的标准方程是
| x2 |
| 4 |
| y2 |
| 3 |
(2)联立
|
由△=12[3m2q2-(3m2+4)(q2-4)]=48(3m2+4-q2)>0
得3m2+4-q2>0①…(7分)
记A(x1,y1),B(x2,y2),
则y1+y2=
| -6mq |
| 3m2+4 |
| 3q2-12 |
| 3m2+4 |
∵F(1,0),∴
| FA1 |
| FB |
因A1,F,B三点共线,
∴(x1-1)y2-(x2-1)(-y1)=0…(10分)
∴(x1-1)y2-(x2-1)(-y1)=(my1+q-1)y2+(my2+q-1)y1
=2my1y2+(q-1)(y1+y2)
=2m•
| 3q2-12 |
| 3m2+4 |
| -6mq |
| 3m2+4 |
=2m•
| 3q-12 |
| 3m2+4 |
解得q=4,m≠0.…(12分)
由①②知A1,F,B三点共线的充要条件是|m|>2且q=4.…(13分)
点评:本题考查椭圆方程的求法,考查三点共线的充要条件的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
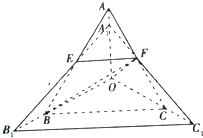 如图,在三棱锥A-BOC中,OA,OB,OC两两垂直,OA=OB=OC=2,E,F分别是棱AB,AC的中点.
如图,在三棱锥A-BOC中,OA,OB,OC两两垂直,OA=OB=OC=2,E,F分别是棱AB,AC的中点.