题目内容
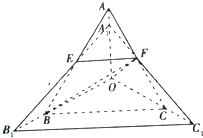如图，在三棱锥A-BOC中，OA，OB，OC两两垂直，OA=OB=OC=2，E，F分别是棱AB，AC的中点．（1）求证：AC⊥平面BOF；
（2）过EF作平面与棱OA，OB，OC或其延长线分别交于点A1，B1，C1，已知OA1=
| 3 |
| 2 |
考点：直线与平面所成的角,直线与平面垂直的判定
专题：空间位置关系与距离,空间角
分析：（1）由已知条件得OB⊥平面AOC，从而AC⊥OB，又AC⊥OF，由此能证明AC⊥平面BOF．
（2）过点O作OP⊥A1B1于点P，连接PC1，由已知得OC⊥A1B1，A1B1⊥平面POC1，过点O作OH⊥PC1于H，由已知得∠PC1O就是直线OC1与平面A1B1C1所成的角．过点F作FD⊥OC1于D，由此能求出直线OC1与平面A1B1C1所成角的正弦值．
（2）过点O作OP⊥A1B1于点P，连接PC1，由已知得OC⊥A1B1，A1B1⊥平面POC1，过点O作OH⊥PC1于H，由已知得∠PC1O就是直线OC1与平面A1B1C1所成的角．过点F作FD⊥OC1于D，由此能求出直线OC1与平面A1B1C1所成角的正弦值．
解答：
（1）证明：因为OB⊥OA，OB⊥OC，OA∩OC=O，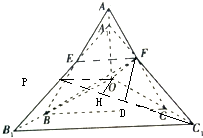
所以OB⊥平面AOC．
因为AC?平面AOC，所以AC⊥OB
因为OA=OC，F是AC的中点，所以AC⊥OF，
又OB∩OF=O，所以AC⊥平面BOF．（5分）
（2）解：过点O作OP⊥A1B1于点P，连接PC1．
已知OC⊥平面AOB，又OP?平面AOB，A1B1?平面AOB，
所以OC⊥OP，OC⊥A1B1．
因为OP⊥A1B1，OP∩OC=O，
所以A1B1⊥平面POC，即A1B1⊥平面POC1，
过点O作OH⊥PC1于H，因为OH?平面POC1，
所以A1B1⊥OH，又A1B1∩PC1=P，所以OH⊥平面A1B1C1，
所以∠PC1O就是直线OC1与平面A1B1C1所成的角．
因为OA=OB=OC=2，OA1=
，
过点F作FD⊥OC1于D，
设CC1=t，由
=
得
=
，
所以t=1，即OC1=3，同理OB1=3（11分）
在Rt△A1OB1中，OP=
=
=
，
在Rt△POC1中，PC1=
=
=
，
所以sin∠PC1O=
=
=
，
即直线OC1与平面A1B1C1所成角的正弦值为
．（15分）
所以OB⊥平面AOC．
因为AC?平面AOC，所以AC⊥OB
因为OA=OC，F是AC的中点，所以AC⊥OF，
又OB∩OF=O，所以AC⊥平面BOF．（5分）
（2）解：过点O作OP⊥A1B1于点P，连接PC1．
已知OC⊥平面AOB，又OP?平面AOB，A1B1?平面AOB，
所以OC⊥OP，OC⊥A1B1．
因为OP⊥A1B1，OP∩OC=O，
所以A1B1⊥平面POC，即A1B1⊥平面POC1，
过点O作OH⊥PC1于H，因为OH?平面POC1，
所以A1B1⊥OH，又A1B1∩PC1=P，所以OH⊥平面A1B1C1，
所以∠PC1O就是直线OC1与平面A1B1C1所成的角．
因为OA=OB=OC=2，OA1=
| 3 |
| 2 |
过点F作FD⊥OC1于D，
设CC1=t，由
| FD |
| OA1 |
| DC1 |
| OC1 |
| 1 | ||
|
| 1+t |
| 2+t |
所以t=1，即OC1=3，同理OB1=3（11分）
在Rt△A1OB1中，OP=
| OA1•OB1 |
| A1B1 |
| ||||
|
| 3 | ||
|
在Rt△POC1中，PC1=
O
|
9+
|
3
| ||
|
所以sin∠PC1O=
| OP |
| PC1 |
| ||||||
|
| ||
| 6 |
即直线OC1与平面A1B1C1所成角的正弦值为
| ||
| 6 |
点评：本题考查直线与平面垂直的证明，考查直线与平面所成角的正弦值的求法，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
名校课堂系列答案
相关题目