题目内容
7.已知函数$f(x)=\sqrt{a{x^2}+ax+3}$的定义域为R,则实数a的取值范围为( )| A. | $({\frac{1}{3},+∞})$ | B. | (0,12] | C. | [0,12] | D. | $({-∞,\frac{1}{3}}]$ |
分析 把函数$f(x)=\sqrt{a{x^2}+ax+3}$的定义域为R转化为ax2+ax+3≥0对任意实数x恒成立,然后对a分类讨论求解得答案.
解答 解:∵函数$f(x)=\sqrt{a{x^2}+ax+3}$的定义域为R,
∴ax2+ax+3≥0对任意实数x恒成立,
当a=0时满足题意;
当a≠0时,则$\left\{\begin{array}{l}{a>0}\\{{a}^{2}-12a≤0}\end{array}\right.$,解得:0<a≤12.
∴实数a的取值范围为[0,12].
故选:C.
点评 本题考查函数的定义域及其求法,考查了数学转化思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,五面体ABCDE中,AB∥CD,CB⊥平面ABE,AE⊥AB,AB=AE=2,BC=$\sqrt{2}$,CD=1.
如图,五面体ABCDE中,AB∥CD,CB⊥平面ABE,AE⊥AB,AB=AE=2,BC=$\sqrt{2}$,CD=1. 如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.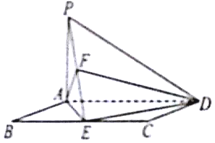 如图,在矩形ABCD中,BC=2AB,PA⊥平面ABCD,E为BC的中点.
如图,在矩形ABCD中,BC=2AB,PA⊥平面ABCD,E为BC的中点.