题目内容
19. 如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.(1)求证:PA∥面BDE;
(2)求证:BD⊥平面PAC.
分析 (1)线面平行转化为线线平行证明,只需在面BDE找一条直线与PA平行即可,连接OE,利用三角形中位线可证.
(2)线面垂直只需证明直线垂直这平面内的两条相交的直线即可.ABCD是正方形,BD⊥AC,PO⊥底面ABCD,可得PO⊥BD,即可证明.
解答 解:(1)ABCD是正方形,O是正方形的中心,即O是BD和AC的中点,E是PC的中点,连接OE,
在三角形APC中,OE∥AP,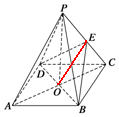
∵OE?面BDE,
∴PA∥面BDE;
(2)∵ABCD是正方形,O是正方形的中心
∴BD⊥AC,
∵PO⊥底面ABCD,
∴PO⊥BD,
∵PO?平面PAC,
AC?平面PAC,
PO∩AC=O,
∴BD⊥平面PAC.
点评 本题考查线面平行转化为线线平行的证明,线面垂直只需证明直线垂直这平面内的两条相交的直线即可.属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
9.设点P(x,y) 在函数y=4-2x的图象上运动,则9x+3y的最小值为( )
| A. | 9 | B. | 12 | C. | 18 | D. | 22 |
10. 在函数y=|x|(x∈[-2,2])的图象上有一点P(t,|t|),此函数的图象与x轴、直线x=-2及x=t围成的图形(如图阴影部分)的面积为S,则S与t的函数关系可表示为( )
在函数y=|x|(x∈[-2,2])的图象上有一点P(t,|t|),此函数的图象与x轴、直线x=-2及x=t围成的图形(如图阴影部分)的面积为S,则S与t的函数关系可表示为( )
 在函数y=|x|(x∈[-2,2])的图象上有一点P(t,|t|),此函数的图象与x轴、直线x=-2及x=t围成的图形(如图阴影部分)的面积为S,则S与t的函数关系可表示为( )
在函数y=|x|(x∈[-2,2])的图象上有一点P(t,|t|),此函数的图象与x轴、直线x=-2及x=t围成的图形(如图阴影部分)的面积为S,则S与t的函数关系可表示为( )| A. |  | B. |  | C. |  | D. |  |
7.已知函数$f(x)=\sqrt{a{x^2}+ax+3}$的定义域为R,则实数a的取值范围为( )
| A. | $({\frac{1}{3},+∞})$ | B. | (0,12] | C. | [0,12] | D. | $({-∞,\frac{1}{3}}]$ |
 《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何.刍甍:底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图,设网格纸上每个小正方形的边长为1丈),那么该刍甍的体积为( )
《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何.刍甍:底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图,设网格纸上每个小正方形的边长为1丈),那么该刍甍的体积为( )