题目内容

12．不等式|x+1|-|x-3|≤a在实数集上有解，则实数a的取值范围为[-4，+∞]．

分析 由绝对值的意义可得|x+1|-|x-3|的最小值为-4，要使不等式|x+1|-|x-3|≤a在实数集上有解，则实数a≥-4．

解答 解：由于|x+1|-|x-3|表示数轴上的x对应点到-1的距离减去它到3对应点的距离，它的最小值为-4，
要使不等式|x+1|-|x-3|≤a在实数集上有解，则实数a≥-4，
故答案为：[-4，+∞）．

点评 本题主要考查绝对值的意义，绝对值不等式的解法，属于中档题．

练习册系列答案
相关题目
2．已知函数f（x）=sin（ωx+φ）-b（ω＞0，0＜φ＜π）的图象两相邻对称轴之间的距离是$\frac{π}{2}$，若将f（x）的图象先向右平移$\frac{π}{6}$个单位，再向上平移$\sqrt{3}$个单位，所得函数g（x）为奇函数．
（1）求f（x）的解析式；
（2）求f（x）的对称轴及单调增区间；
（3）若对任意x∈[0，$\frac{π}{3}$]，f2（x）-（2+m）f（x）+2+m≤0恒成立，求实数m的取值范围．
3．若函数y=f（x）对任意的x，y∈R，恒有f（x+y）=f（x）+f（y）．当x＞0时，恒有f（x）＜0．
（1）判断函数f（x）的奇偶性，并证明你的结论；
（2）若f（2）=1，解不等式f（-x2）+2f（x）+4＜0．
20．已知$a_1^2+b_1^2≠0$，$a_2^2+b_2^2≠0$，则“$|{\begin{array}{l}{a_1}&{b_1}\\{{a_2}}&{b_2}\end{array}}|≠0$”是“直线a1x+b1y+c1=0与直线a2x+b2y+c2=0”平行的（　　）条件．
A．充分不必要B．必要不充分
C．充要D．既不充分也不必要
7．已知函数$f（x）=\sqrt{a{x^2}+ax+3}$的定义域为R，则实数a的取值范围为（　　）
A．$（{\frac{1}{3}，+∞}）$B．（0，12]C．[0，12]D．$（{-∞，\frac{1}{3}}]$
17．某四棱锥的三视图如图所示，则该四棱锥的表面积为（　　）
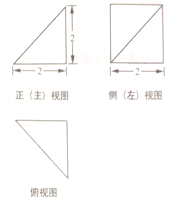
A．$8+4\sqrt{2}$B．$6+\sqrt{2}+2\sqrt{3}$C．$6+4\sqrt{2}$D．$6+2\sqrt{2}+2\sqrt{3}$
4．设命题p：关于x的不等式ax＜1的解集是{x|x＜0}；
命题q：?x0∈R，ax02+4x0+a≤0．若￢p∨q为假命题，求实数a的取值范围．
1．已知函数f（x）=$\sqrt{3}$sin（x+θ）+cos（x+θ）$（θ∈[-\frac{π}{2}，\frac{π}{2}]）$是偶函数，则θ的值为$\frac{π}{3}$．
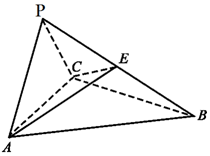2．如图，三棱锥P-ABC中，△ABC是正三角形，△ACP是直角三角形，∠ABP=∠CBP，AB=BP．
（1）证明：平面ACP⊥平面ABC；
（2）若E为棱PB与P不重合的点，且AE⊥CE，求AE与平面ABC所成的角的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网